What is the pressure in an ocean at a depth of 1000 m, if the density of water is . Atmospheric pressure Pa.
To find the pressure in an ocean at a depth of 1000 m, we can use the formula for absolute pressure at a certain depth, which is given by:
P=Patmospheric+ρgh
Where:
- P is the absolute pressure at depth,
- Patmospheric is the atmospheric pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid.
1. Identify the Given Values:
- Depth h=1000m
- Density of water ρ=1.024×103kg/m3
- Atmospheric pressure Patmospheric=1.01×105Pa
- Acceleration due to gravity g≈10m/s2
2. Calculate the Pressure Due to the Water Column:
- Use the formula for pressure due to a column of fluid:
Pwater=ρgh
- Substitute the values:
Pwater=(1.024×103kg/m3)(10m/s2)(1000m)
- Calculate:
Pwater=1.024×103×10×1000=1.024×107Pa
3. Convert Pwater to a Standard Form:
- Pwater=1.024×107Pa=10.24×106Pa
4. Calculate the Total Absolute Pressure:
- Now, add the atmospheric pressure to the pressure due to the water column:
P=Patmospheric+Pwater
- Substitute the values:
P=(1.01×105Pa)+(1.024×107Pa)
- Convert Patmospheric to the same order of magnitude:
Patmospheric=0.101×107Pa
- Now add:
P=(0.101×107)+(1.024×107)=1.125×107Pa
5. Express the Final Answer:
- The final pressure at a depth of 1000 m is:
P=1.125×107Pa=112.5×105Pa
Final Answer:
The pressure in the ocean at a depth of 1000 m is approximately 1.125×107Pa or 112.5×105Pa.
- P is the absolute pressure at depth,
- Patmospheric is the atmospheric pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid.
- Depth h=1000m
- Density of water ρ=1.024×103kg/m3
- Atmospheric pressure Patmospheric=1.01×105Pa
- Acceleration due to gravity g≈10m/s2
- Use the formula for pressure due to a column of fluid:
Pwater=ρgh
- Substitute the values:
Pwater=(1.024×103kg/m3)(10m/s2)(1000m)
- Calculate:
Pwater=1.024×103×10×1000=1.024×107Pa
- Pwater=1.024×107Pa=10.24×106Pa
- Now, add the atmospheric pressure to the pressure due to the water column:
P=Patmospheric+Pwater
- Substitute the values:
P=(1.01×105Pa)+(1.024×107Pa)
- Convert Patmospheric to the same order of magnitude:
Patmospheric=0.101×107Pa
- Now add:
P=(0.101×107)+(1.024×107)=1.125×107Pa
- The final pressure at a depth of 1000 m is:
P=1.125×107Pa=112.5×105Pa
The pressure in the ocean at a depth of 1000 m is approximately 1.125×107Pa or 112.5×105Pa.
Topper's Solved these Questions
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
16 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - LONG ANSWER QUESTIONS
5 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
Similar Questions
At a depth of 500m in an ocean (a) what is the absolute pressure? (b) What is the gauge pressure? Density of sea water is 1.03×103kg/m3,g=10ms−2. Atmospheric pressure = 1.01×105Pa.
View SolutionAt a depth of 1000 m in an ocean (a) what is the absolute pressure? (b) what is the gauge pressure? (c ) Find the force acting on the window of area 20cm×20cm of a submarine at this depth, the interior of which is maintained at sea-level atmospheric pressure. The density of sea water is 1.03×103kgm−3, g=10ms−2. Atmospheric pressure = 1.01×105Pa.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionThe curved wall of a dam is described by the equation
x2=2y
The coordinates of point A are (4m,8m) . The width of the dam is 2m and the fluid is water of density 1×103kg/m3
Atmospheric pressure is 1.0×105 Pa
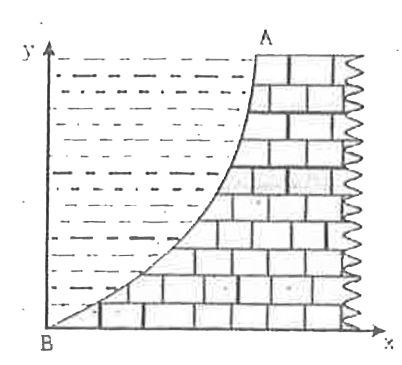
The horizontal component of the force applied by the liquid on the surface AB is (g=10ms−2)
View SolutionThe curved wall of a dam is described by the equation
x2=2y
The coordinates of point A are (4m,8m) . The width of the dam is 2m and the fluid is water of density 1×103kg/m3
Atmospheric pressure is 1.0×105 Pa
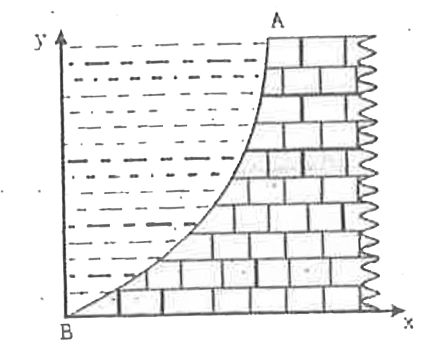
the vertical component of the force applied by the liquid on the surface is
View SolutionWhat is the pressure on a swimmer 10m below the surface of lake? g=10ms−2, atmospheric pressure = 1.01×105Pa
View SolutionWhat is the maximum possible sound level in dB of sound waves in air? Given that density of air is 1.3kgm3, v=332ms and atmospheric pressure P=1.01×105Nm2.
View SolutionWhat is the density of ocean water at a depth, where the pressure is 80.0 atm, given that its density at the surface is 1.03×103kgm−3? Compressibilty of water =45.8×10−11Pa−1. Given 1 atm. =1.013×105Pa.
View SolutionThe guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
View SolutionWhat is the density of ocean water at a depth, where the pressure is 80.0atm, given that is density at the surface is 1.03×103kgm−3 ( compressibility of water =45.8×10−11Pa−1 ) ?
View Solution
