Question

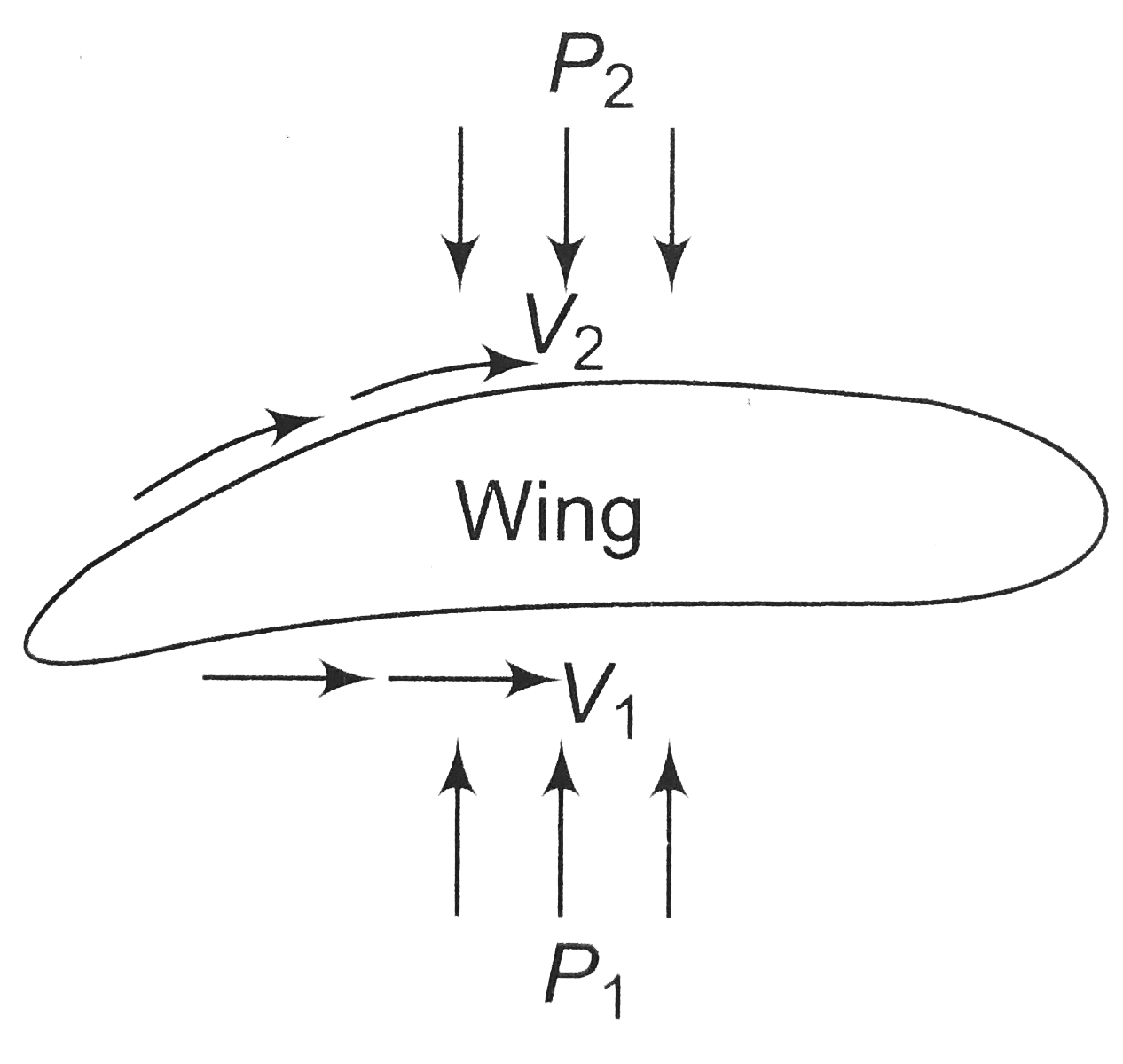
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are $70m{s}^{-1}\text{and}63m{s}^{-1}$ respectively. What is the lift on the wing if its area is$2.5m^2$? Take the density of air to be$1.3kg{m}^{-3}$

Answer

` 1512 . 9 N`

Explanation

To solve the problem of calculating the lift on the wing of a model aeroplane in a wind tunnel, we can use Bernoulli's principle. Here’s a step-by-step breakdown of the solution:

Step 1: Understand the Given Information
- Speed on the upper surface of the wing, \( V_1 = 70 \, \text{m/s} \)
- Speed on the lower surface of the wing, \( V_2 = 63 \, \text{m/s} \)
- Area of the wing, \( A = 2.5 \, \text{m}^2 \)
- Density of air, \( \rho = 1.3 \, \text{kg/m}^3 \)

Step 2: Apply Bernoulli's Equation
According to Bernoulli’s principle, the difference in pressure between the upper and lower surfaces of the wing can be expressed as:
\( \Delta P = \frac{1}{2} \rho (V_2^2 - V_1^2) \)
Where:
- \( \Delta P \) is the pressure difference,
- \( V_1 \) is the velocity of air over the upper surface,
- \( V_2 \) is the velocity of air over the lower surface.

Step 3: Calculate the Pressure Difference
Substituting the values into the equation:
\( \Delta P = \frac{1}{2} \times 1.3 \, \text{kg/m}^3 \times (63^2 - 70^2) \)

Calculating \( 63^2 \) and \( 70^2 \):
\( 63^2 = 3969 \quad \text{and} \quad 70^2 = 4900 \)
Now, calculate the difference:
\( 63^2 - 70^2 = 3969 - 4900 = -931 \)
Now substituting back into the pressure difference equation:
\( \Delta P = \frac{1}{2} \times 1.3 \times (-931) \)
Calculating this gives:
\( \Delta P = \frac{1}{2} \times 1.3 \times -931 = -605.15 \, \text{Pa} \)
Taking the absolute value:
\( |\Delta P| = 605.15 \, \text{Pa} \)

Step 4: Calculate the Lift Force
The lift force \( F_{\text{lift}} \) can be calculated using the formula:
\( F_{\text{lift}} = \Delta P \times A \)
Substituting the values:
\( F_{\text{lift}} = 605.15 \, \text{Pa} \times 2.5 \, \text{m}^2 \)
Calculating this gives:
\( F_{\text{lift}} = 1512.875 \, \text{N} \)

Final Answer
The lift on the wing is approximately:
\( F_{\text{lift}} \approx 1512.87 \, \text{N} \)