A capillary tube PQ of length 0.6 m and radius 4×10−3m is connected in series with another capillary tube QS of length 0.45 m and radius 10−3m. The tubes are arranged horizontally. End P is connected to a vessel of water having constant pressure head of 0.8 m. The end S is open to the atmosphere. Find the pressure at the junction Q ?
The correct Answer is:0.7939m of water
To solve the problem step by step, we will analyze the capillary tubes and apply the principles of fluid mechanics.
Step 1: Understand the System
We have two capillary tubes, PQ and QS, connected in series. The pressure at point P is due to a water column of height 0.8 m. The pressure at point S is atmospheric pressure (P0).
Step 2: Define the Pressures
- Pressure at Point P (PP): This is the pressure due to the water column. It can be calculated using the formula:
PP=P0+ρgh
where h=0.8m, ρ is the density of water (approximately 1000kg/m3), and g is the acceleration due to gravity (approximately 9.81m/s2).
Step 3: Calculate Pressure at Point P
Substituting the values:
PP=P0+(1000kg/m3)(9.81m/s2)(0.8m)
Calculating ρgh:
ρgh=1000×9.81×0.8=7848Pa
Thus,
PP=P0+7848Pa
Step 4: Define the Pressure at Point S
- Pressure at Point S (PS): Since point S is open to the atmosphere, we have:
PS=P0
Step 5: Apply Poiseuille’s Law
For both tubes, we can apply Poiseuille's law, which states that the flow rate Q is given by:
Q=π(P2−P1)r48ηL
where P2 and P1 are the pressures at the two ends of the tube, r is the radius, η is the viscosity of the fluid, and L is the length of the tube.
Step 6: Set Up Equations for Each Tube
1. For tube PQ:
QPQ=π(PP−PQ)(4×10−3)48η(0.6)
2. For tube QS:
QQS=π(PQ−PS)(1×10−3)48η(0.45)
Step 7: Equate the Flow Rates
Since the tubes are in series, the flow rates are equal:
(PP−PQ)(4×10−3)40.6=(PQ−PS)(1×10−3)40.45
Step 8: Substitute Known Values
Substituting PP and PS:
(P0+7848−PQ)(4×10−3)40.6=(PQ−P0)(1×10−3)40.45
Step 9: Solve for PQ
This equation can be solved for PQ. After simplification, we will find the pressure at junction Q.
Step 10: Final Calculation
After performing the calculations, we will arrive at the pressure at junction Q.
We have two capillary tubes, PQ and QS, connected in series. The pressure at point P is due to a water column of height 0.8 m. The pressure at point S is atmospheric pressure (P0).
- Pressure at Point P (PP): This is the pressure due to the water column. It can be calculated using the formula:
PP=P0+ρgh
where h=0.8m, ρ is the density of water (approximately 1000kg/m3), and g is the acceleration due to gravity (approximately 9.81m/s2).
Substituting the values:
PP=P0+(1000kg/m3)(9.81m/s2)(0.8m)
Calculating ρgh:
ρgh=1000×9.81×0.8=7848Pa
Thus,
PP=P0+7848Pa
- Pressure at Point S (PS): Since point S is open to the atmosphere, we have:
PS=P0
For both tubes, we can apply Poiseuille's law, which states that the flow rate Q is given by:
Q=π(P2−P1)r48ηL
where P2 and P1 are the pressures at the two ends of the tube, r is the radius, η is the viscosity of the fluid, and L is the length of the tube.
1. For tube PQ:
QPQ=π(PP−PQ)(4×10−3)48η(0.6)
2. For tube QS:
QQS=π(PQ−PS)(1×10−3)48η(0.45)
Since the tubes are in series, the flow rates are equal:
(PP−PQ)(4×10−3)40.6=(PQ−PS)(1×10−3)40.45
Substituting PP and PS:
(P0+7848−PQ)(4×10−3)40.6=(PQ−P0)(1×10−3)40.45
This equation can be solved for PQ. After simplification, we will find the pressure at junction Q.
After performing the calculations, we will arrive at the pressure at junction Q.
Topper's Solved these Questions
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS ( FROM VISCOSITY , STOKES LAW)
Explore 17 Videos
- INTERNAL ENERGY Book:ICSEChapter:INTERNAL ENERGY Exercise:SELECTED PROBLEMS (FROM HEAT ENGINES)
Explore 21 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
Similar Questions
The rate of steady volume flow of water through a capillary tube of length ' l ' and radius ' r ' under a pressure difference of P is V . This tube is connected with another tube of the same length but half the radius in series. Then the rate of steady volume flow through them is (The pressure difference across the combination is P )
View SolutionA glass rod of radius 1mm is inserted symmetrically into a glass capillary tube with inside radius 2mm. Then the whole arrangement is brought in contact of the surface of water. Surface tension of water is 7×10−2N/m. To what height will the water rise in the capillary? (θ=0∘)
View Solution
Knowledge Check
Two capillaries of same length and radii in the ratio 1:2 are connected in series. A liquid flows through them in streamlined condition. If the pressure across the two extreme ends of the combination is 1 m of water, the pressure difference across first capillary is
A9.4 mB4.9 mC0.49 mD0.94 m
Figure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
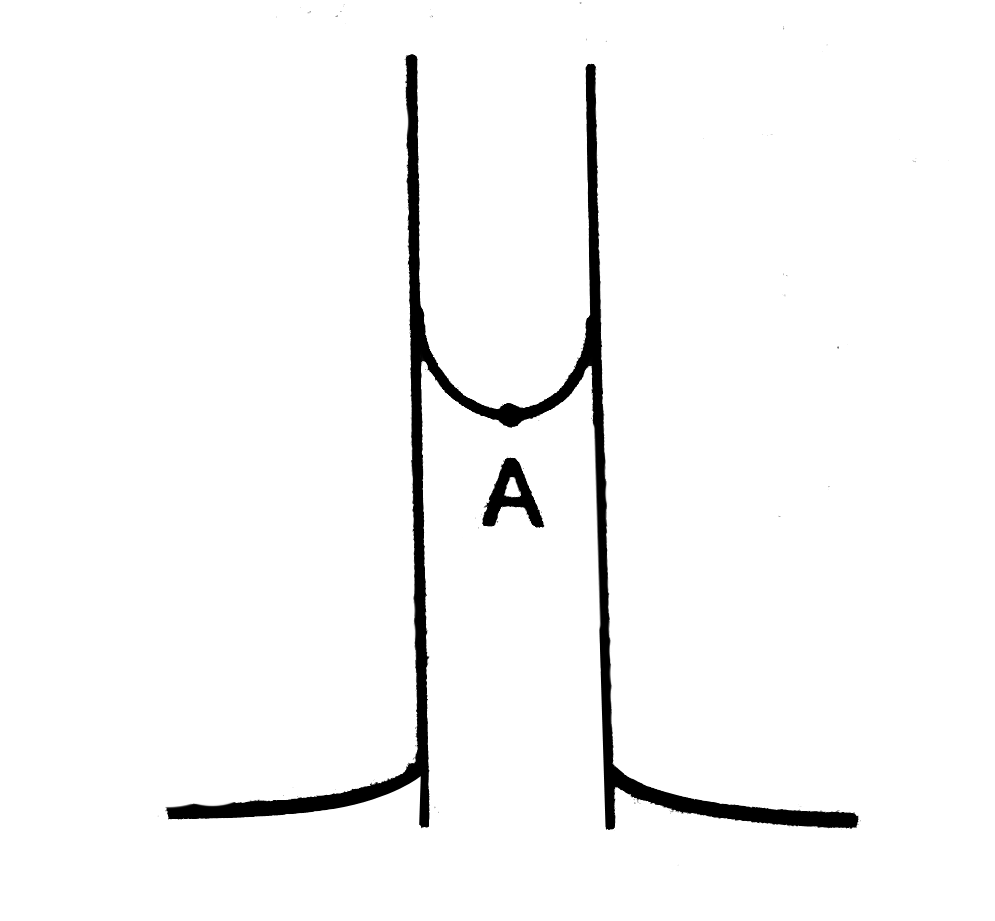
View SolutionA capillary tube of length 5 cm and diameter 1 mm is connected to a tank horizontally. The rate of flow of water is 10 ce per minute. Calculate the rate of flow of water through another capillary tube of diameter 2 mm and length 50 cm is connected in series with the first capillary?
View SolutionWhen a capillary tube is immersed in a liquid, then liquid of mass M rises in the capillary tube.^lf capillary tube of double radius is taken then mass of same liquid rising in the tube is
View Solution16cm3 of water flows per second through a capillary tube of radius a cm and of length l cm when connected to a pressure head of h cm of water if a tube of the same length and radius a/2 cm is connected to the same pressure head the quantity of water flowing through the tube per second will be-
View SolutionWater is flowing through a horizontal tube of length 0.25 m and radius 4×10−4 m under a constant pressure head of 0.2 m of water, at the rate of 5×10−6m3 per minutre . Calculate the coefficient of visosity of water. Density of water = 1000 kg m−3
View SolutionA capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
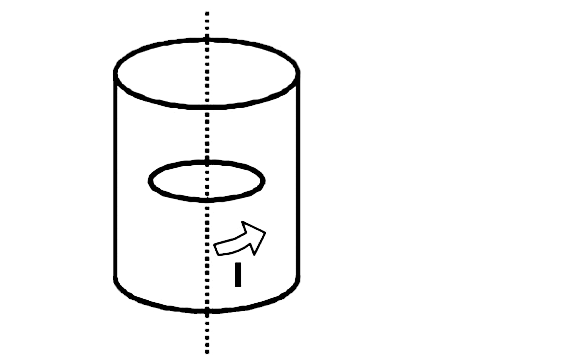
View SolutionA long circular tube of length 10m and radius 0.3m carries a current I along its curved surface as shown . A wire - loop of resistance 0.005ohm and of radius 0.1m is placed inside the tube its axis coinciding with the axis of the tube . The current varies as I=I0cos(300t) where I0 is constant. If the magnetic moment of the loop is Nμ0I0sin(300t), then 'N' is
View Solution

