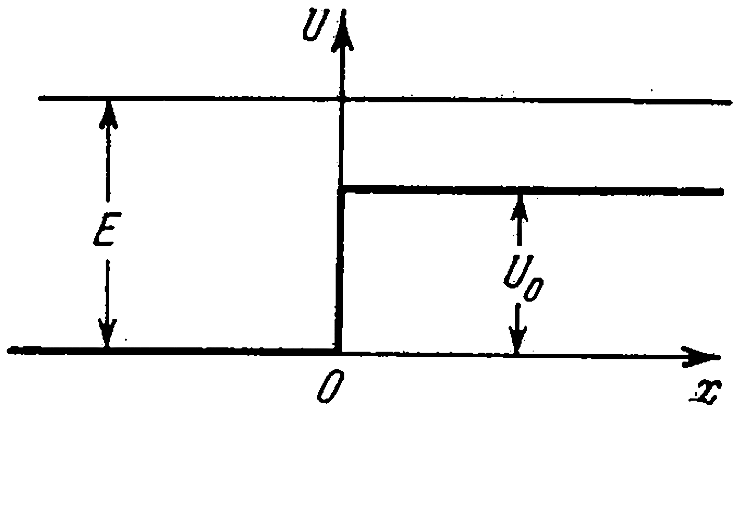
Particles of mass m and energy E move from the left to the potential barrier shown in Fig. 6.3. Find:a the reflection coefficient R of the barrier for E > U0;b the effective penetration depth of the particles into the region x > 0 for E < Uo i.e. the distance from the barrier boundary to the point at which the probability of finding a particle decreases e-fold.
In region I x < 0 the amplitude of eikx is written as unity by convention. In II we expect only a transmitted wave to the right B = 0 then. So
Related Solutions
Particle of mass and energy moves from the left to the potential barrier shown in figure. Find:
(a) the reflection coefficient of the barrier for
(b) the effective penetration depth of the particles into the region for i.e., the distacne from the barrier boundary to the point at which the probability of finding a particle decreases e-fold
View SolutionUsing Eq.(6.2e), find the probability of a particle of mass and energy tunneling through the potential barrier shown in fig. where .
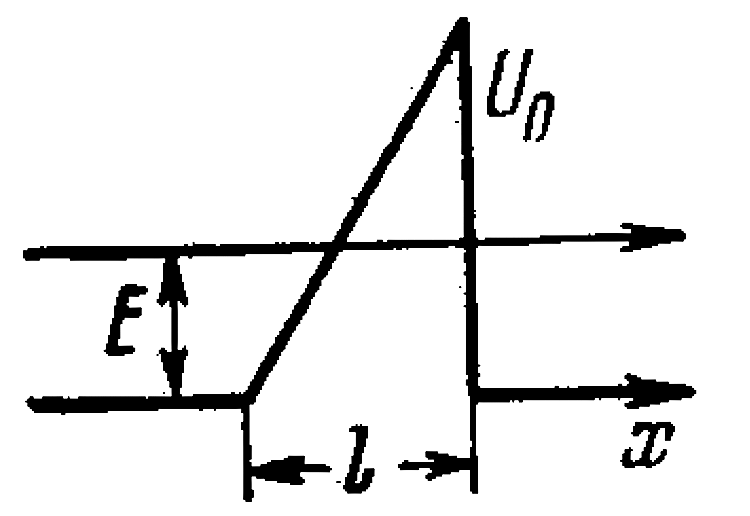
View SolutionEmploying Eq.(6.2e), find the probability of an electron with energy tunneling through a potential barrier of width and height provided the barrier is shaped as shown:
(a) In fig 6.4
(b) in figure 6.5.
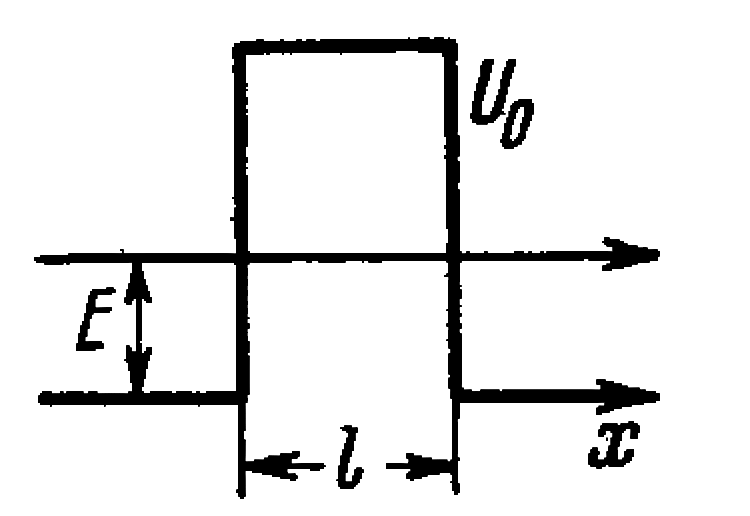
View Solutionपृथ्वी तल पर द्रव्यमान m के कण की स्थितिज ऊर्जा है | पृथ्वी तल से ऊँचाई पर कण की स्थितिज ऊर्जा होगी :
View SolutionA particle with total energy E is moving in a potential energy region U (x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x).Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionTh e barrier potential of a silicon diode is approximately,
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
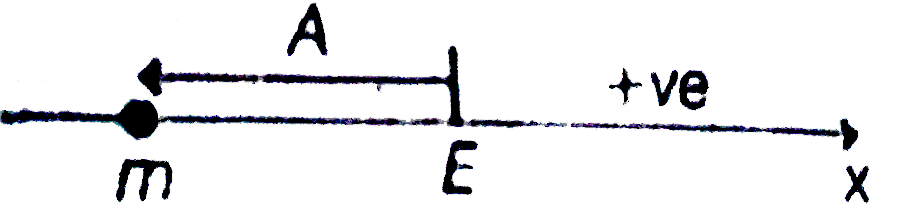
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
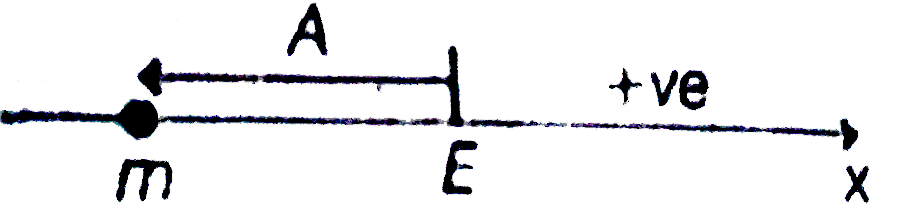
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0. Velocity-time graph of the particle is
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
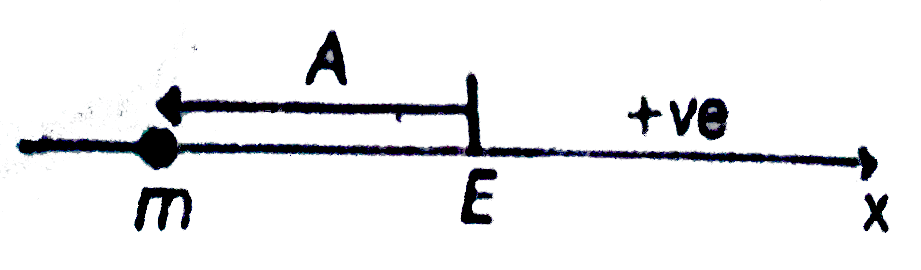
View Solutionएक सरल आवर्त गति करते कण की स्थितिज ऊर्जा , जब कण अपने अंतिम बिंदु से आधी दूरी पर है, होगी ( E= कुल ऊर्जा )
View SolutionAn electron with energy E is incident upon a potential energy barrier of height and thickness L. The transmission coefficient T
View SolutionAn electron with energy E is incident on a potential energy barrier of height and thickness L. The probability of tunneling increases if
View SolutionA particle with total energy moves in one direction in a region where, the potential energy is The acceleration of the particle is zero, where,
View SolutionA particle with total energy moves in one direction in a region where, the potential energy is The acceleration of the particle is zero, where,
View SolutionA particle with total energy moves in one direction in a region where, the potential energy is The acceleration of the particle is zero, where,
View Solutionद्रव्यमान m के एक कण को वेग से ऊपर की ओर प्रक्षेपित किया जाता है, जहां पलायन वेग है, तब अधिकतम ऊँचाई पर कण की स्थितिज ऊर्जा है: (R पृथ्वी की त्रिज्या है और M पृथ्वी का द्रव्यमान है)
View Solution