A particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
U=E
U=0
dUdx=0
d2Udx2=0
The correct Answer is:C
To solve the problem, we need to analyze the conditions under which the acceleration of a particle is zero. Here’s the step-by-step solution:
Step 1: Understand the relationship between force and potential energy
The force acting on a particle in a potential energy field is given by the negative gradient of the potential energy. Mathematically, this is expressed as:
F=−dUdx
where U is the potential energy and x is the position.
Step 2: Set the condition for zero acceleration
For a particle to have zero acceleration, the net force acting on it must also be zero. Therefore, we set the force equation to zero:
F=0
Step 3: Substitute the force equation
From the force equation, we have:
−dUdx=0
Step 4: Solve for the potential energy gradient
To satisfy the equation, we need:
dUdx=0
This indicates that the potential energy U is constant with respect to position x.
Step 5: Conclusion
Thus, the acceleration of the particle is zero when the derivative of the potential energy with respect to position is zero. This means that in the region where the particle is moving, the potential energy does not change with position.
Final Answer:
The acceleration of the particle is zero where:
dUdx=0
---
The force acting on a particle in a potential energy field is given by the negative gradient of the potential energy. Mathematically, this is expressed as:
F=−dUdx
where U is the potential energy and x is the position.
For a particle to have zero acceleration, the net force acting on it must also be zero. Therefore, we set the force equation to zero:
F=0
From the force equation, we have:
−dUdx=0
To satisfy the equation, we need:
dUdx=0
This indicates that the potential energy U is constant with respect to position x.
Thus, the acceleration of the particle is zero when the derivative of the potential energy with respect to position is zero. This means that in the region where the particle is moving, the potential energy does not change with position.
The acceleration of the particle is zero where:
dUdx=0
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
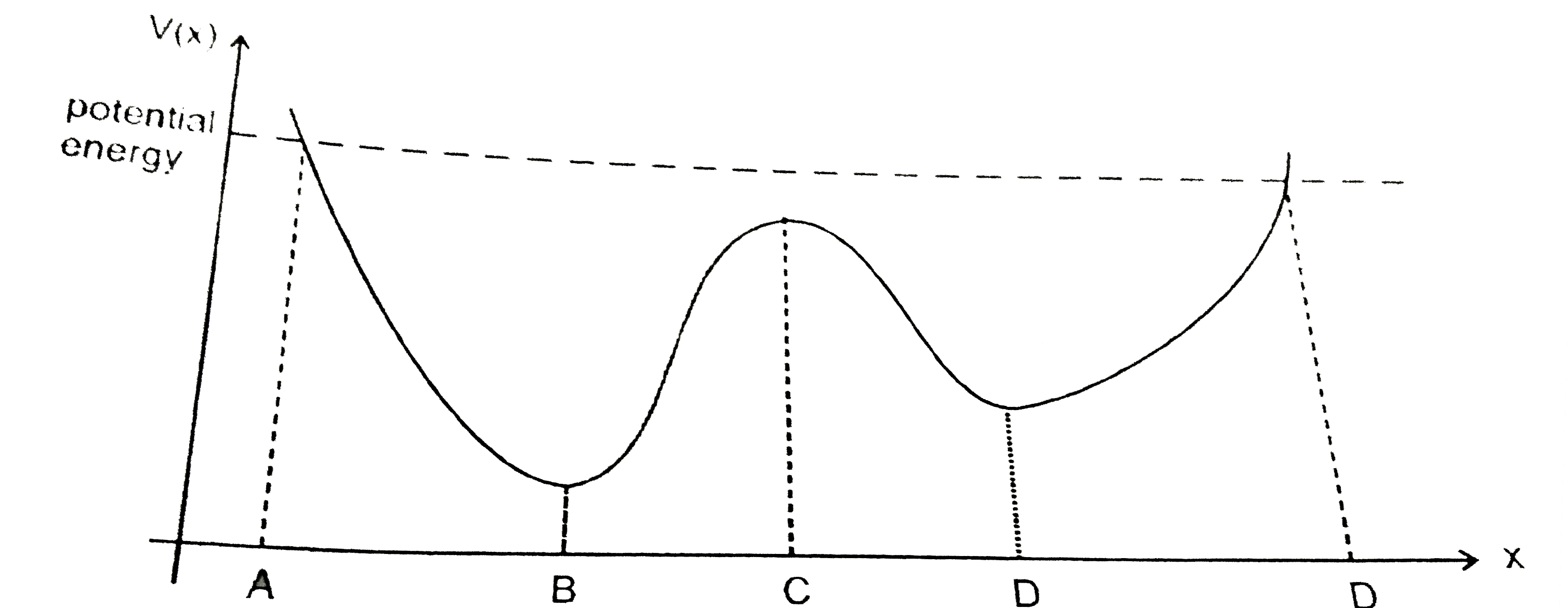
If the particle starts to move from rest from the point A, then
View SolutionA particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.

If the particle starts to move from rest from the point A, then
View Solution
Knowledge Check
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D is which the relation between potential energy U, kinetic energy (K) and total energy E is as given below
RegionA:U>E Region B:U<E
Region C:K<E Region D:U>E
State with reason in each case whether a particle can be found in the given region or not.ARegion ABRegion BCRegion CDRegion D
A particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View SolutionConsider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D is which the relation between potential energy U, kinetic energy (K) and total energy E is as given below
RegionA:U>E Region B:U<E
Region C:K<E Region D:U>E
State with reason in each case whether a particle can be found in the given region or not.
View SolutionIn position A kinetic energy of a particle is 60 J and potential energy is -20 J. In position B, kinetic energy is 100 J and potential energy is 40 J. Then, in moving the particle from A to B
View SolutionA particle executes linear SHM with amplitude A and mean position is x=0. Determine position of the particle where potential energy of the particle is equal to its kinetic energy.
View SolutionA particle with the potentila energy shown in the graph is moving to the right. It has 1.0J of kinetic energy at x=1.0m. Where the particle reverses its direction of motion?

View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View Solution
