An electron with energy E is incident on a potential energy barrier of height and thickness L. The probability of tunneling increases if
E decreases without any other changes
increases without any other changes
L decreases without any other changes
E and increase by the same amount
The correct Answer is:C
To solve the problem regarding the tunneling probability of an electron encountering a potential energy barrier, we can follow these steps:
1. Understanding the Problem:
- We have an electron with energy E approaching a potential energy barrier of height Epot and thickness L.
- We need to determine the conditions under which the probability of tunneling through this barrier increases.
2. Condition for Tunneling:
- Tunneling occurs when the energy of the electron E is greater than the potential energy barrier Epot. Thus, for tunneling to happen, we require:
E>Epot
3. Transmission Coefficient:
- The probability of tunneling can be quantified using the transmission coefficient T. According to the WKB approximation, the transmission coefficient is given by:
T∝e−2γL
- Where γ is a function of the mass of the electron m and the difference between the energy of the electron and the potential barrier:
γ=√2m(Epot−E)ℏ2
4. Effect of Barrier Thickness L:
- From the equation T∝e−2γL, we can see that as the thickness L increases, the exponent becomes more negative, leading to a decrease in T.
- Conversely, if L decreases, T increases.
5. Conclusion:
- The probability of tunneling increases if the thickness L of the barrier decreases. Therefore, the answer to the question is:
The probability of tunneling increases if L decreases.
- We have an electron with energy E approaching a potential energy barrier of height Epot and thickness L.
- We need to determine the conditions under which the probability of tunneling through this barrier increases.
- Tunneling occurs when the energy of the electron E is greater than the potential energy barrier Epot. Thus, for tunneling to happen, we require:
E>Epot
- The probability of tunneling can be quantified using the transmission coefficient T. According to the WKB approximation, the transmission coefficient is given by:
T∝e−2γL
- Where γ is a function of the mass of the electron m and the difference between the energy of the electron and the potential barrier:
γ=√2m(Epot−E)ℏ2
- From the equation T∝e−2γL, we can see that as the thickness L increases, the exponent becomes more negative, leading to a decrease in T.
- Conversely, if L decreases, T increases.
- The probability of tunneling increases if the thickness L of the barrier decreases. Therefore, the answer to the question is:
The probability of tunneling increases if L decreases.
Topper's Solved these Questions
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 5 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS (Link Comprehension)
Explore 17 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PROBLEMS
Explore 50 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Practice Questions
Explore 57 Videos
- RELATIVITYBook:RESNICK AND HALLIDAYChapter:RELATIVITYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
An electron with total energy E = 5.1 eV approaches a barrier of height Uh=6.8eV and thickness L = 750 pm. What percentage change in the transmission coefficient T occurs for a 1.0% change in (a) the barrier height, (b) the barrier thickness, and (c) the kinetic energy of the incident electron?
View SolutionEmploying Eq.(6.2e), find the probability D of an electron with energy E tunneling through a potential barrier of width l and height U0 provided the barrier is shaped as shown:
(a) In fig 6.4
(b) in figure 6.5.
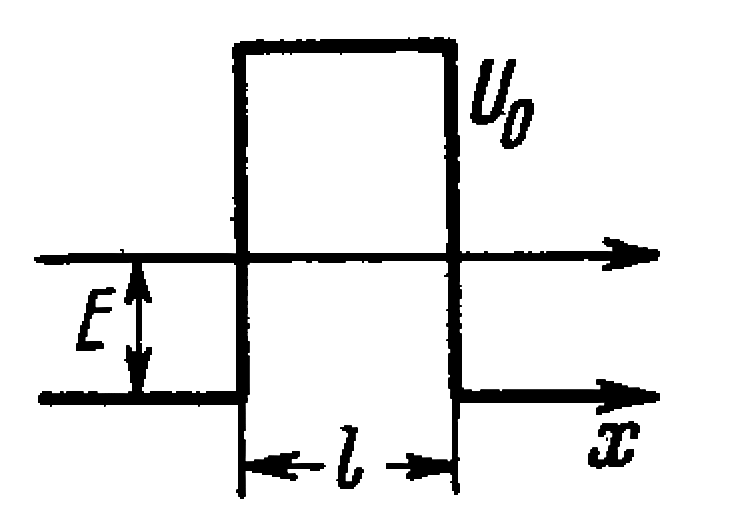

View Solution
Knowledge Check
An electron with energy E is incident upon a potential energy barrier of height Epot>E and thickness L. The transmission coefficient T
AIs zeroBDecreases exponentially with LCIs proportional to 1/LDIs proportional to 1/L2When electron is incident on molyblednum then by changing energy of electron :-
Aλmin changesBλmin remains constantCλKα,λKβ changesDλmin,λKα all changesAn electron is confined to a tube of length L. The electron’s potential energy in one half of the tube is zero, while the potential energy in the other half is 10eV. If the electron has a total energy E=15eV, then the ratio of the deBroglie wavelength of the electron in the 10eV region of the tube to that in the other half is -
A1/√3B√3C3D13
Suppose that the electron in Fig. having a total energy E of 5.1 eV, approaches a barrier of height Ub=6.8eV and thickness L = 750 pm.
(a) What is the approximate probability that the electron will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
(b) What is the approximate probability that a proton with the same total energy of 5.1 eV will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
View SolutionParticle of mass m and energy E moves from the left to the potential barrier shown in figure. Find:
(a) the reflection coefficient R of the barrier for E>U0
(b) the effective penetration depth of the particles into the region x>0 for E<U0i.e., the distacne from the barrier boundary to the point at which the probability of finding a particle decreases e-fold

View SolutionExplain with the help of potential energy barrier how
does a catalyst increase the speed of a reaction ?
View SolutionCheck the sentence true or false:- While climbing a tree Allauddin's height increases from the ground . The potential energy is directly proportional to height of the body from the ground . Therefore , potential energy of Allauddin increases gradually.
View SolutionKinetic energy of a particle on the surface is e0 and potential energy is−E02.
(a) Will the particle escape to infinity ?
(b) At some height some height its kinetic energy becomes 0.6E0. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View Solution