An electron with total energy E = 5.1 eV approaches a barrier of height Uh=6.8eV and thickness L = 750 pm. What percentage change in the transmission coefficient T occurs for a 1.0% change in (a) the barrier height, (b) the barrier thickness, and (c) the kinetic energy of the incident electron?
To solve the problem, we need to analyze the transmission coefficient T for an electron tunneling through a potential barrier. The transmission coefficient is given by:
T=e−2γL
where γ is defined as:
γ=√8π2m(Uh−E)h2
Here, Uh is the height of the barrier, E is the energy of the electron, m is the mass of the electron, h is Planck's constant, and L is the thickness of the barrier.
Step 1: Calculate γ
First, we calculate γ using the given values:
- E=5.1eV
- Uh=6.8eV
Convert eV to Joules (1 eV = 1.6×10−19J):
- E=5.1×1.6×10−19J=8.16×10−19J
- Uh=6.8×1.6×10−19J=1.088×10−18J
Now, calculate Uh−E:
Uh−E=1.088×10−18−8.16×10−19=2.72×10−19J
Now, substituting into the formula for γ:
γ=√8π2m(Uh−E)h2
Using:
- m=9.11×10−31kg
- h=6.626×10−34Js
Substituting these values gives:
γ=
⎷8π2(9.11×10−31)(2.72×10−19)(6.626×10−34)2
Calculating this will yield the value of γ.
Step 2: Find the percentage change in T for a 1% change in barrier height Uh
For a small change in Uh, we can express the change in T as:
ΔTT=−2LΔγγ
Where Δγ can be found by differentiating γ with respect to Uh:
Δγ=dγdUhΔUh
Calculating dγdUh:
dγdUh=12√8π2m(Uh−E)h2⋅8π2mh2
Substituting Uh and E gives the derivative, and then substituting ΔUh=0.01Uh into the equation will yield the percentage change in T.
Step 3: Find the percentage change in T for a 1% change in barrier thickness L
Using the same formula:
ΔTT=−2γΔLL
Substituting ΔL=0.01L will yield the percentage change in T.
Step 4: Find the percentage change in T for a 1% change in kinetic energy E
For a small change in E:
ΔTT=−2LΔγγ
Calculating Δγ with respect to E:
Δγ=dγdEΔE
Where ΔE=0.01E. The derivative dγdE can be calculated similarly as above.
Summary of Results
1. Percentage change in T for 1% change in barrier height: Calculate using the derivative and substitute values.
2. Percentage change in T for 1% change in barrier thickness: Directly substitute into the equation.
3. Percentage change in T for 1% change in kinetic energy: Calculate using the derivative with respect to E.
- E=5.1eV
- Uh=6.8eV
- E=5.1×1.6×10−19J=8.16×10−19J
- Uh=6.8×1.6×10−19J=1.088×10−18J
Uh−E=1.088×10−18−8.16×10−19=2.72×10−19J
γ=√8π2m(Uh−E)h2
- m=9.11×10−31kg
- h=6.626×10−34Js
γ=
⎷8π2(9.11×10−31)(2.72×10−19)(6.626×10−34)2
ΔTT=−2LΔγγ
Δγ=dγdUhΔUh
dγdUh=12√8π2m(Uh−E)h2⋅8π2mh2
ΔTT=−2γΔLL
Substituting ΔL=0.01L will yield the percentage change in T.
ΔTT=−2LΔγγ
Δγ=dγdEΔE
2. Percentage change in T for 1% change in barrier thickness: Directly substitute into the equation.
3. Percentage change in T for 1% change in kinetic energy: Calculate using the derivative with respect to E.
Topper's Solved these Questions
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 47 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 5 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:Check points
Explore 3 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Practice Questions
Explore 57 Videos
- RELATIVITYBook:RESNICK AND HALLIDAYChapter:RELATIVITYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
Suppose that the electron in Fig. having a total energy E of 5.1 eV, approaches a barrier of height Ub=6.8eV and thickness L = 750 pm.
(a) What is the approximate probability that the electron will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
(b) What is the approximate probability that a proton with the same total energy of 5.1 eV will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
View SolutionA technique called photelectron spectroscopy is used to measure the I.P of atoms. A same is irradiated with U.V light, and electrons are ejected from the valence shell. The kinetic energy of the ejected electrons are measured. Since, the energy of the U.V. photon and the kinetic energy of the ejected electrons are known, we can write
hv=I.P.+12mu2
Where v is the frequency of the U.V light, and m and u are mass and velocity of the electron respectively. In one experiment the kinetic energy of the ejected electron from potassium is found to be. 5.34×10−19J using U.V. source of wavelength 162 nm. Calculate I.E. of potassium (h=6.62×10−34J−s,c=3×108m / s).
View Solution
Knowledge Check
An electron with energy E is incident upon a potential energy barrier of height Epot>E and thickness L. The transmission coefficient T
AIs zeroBDecreases exponentially with LCIs proportional to 1/LDIs proportional to 1/L2An electron with energy E is incident on a potential energy barrier of height Epot and thickness L. The probability of tunneling increases if
AE decreases without any other changesBEpot increases without any other changesCL decreases without any other changesDE and Epot increase by the same amount
Light form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quatum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
View SolutionThe work function for a metal is 1.8eV. Light of 5000Å is incident on it. Calculate (a) threshold frequency and threshold wavelength, (b) maximum kinetic energy of the emitted electrons, (c) maximum velocity of the emitted electrons, (d) if the intensity of the incident light be doubled, then what will be the maximum kinetic energy of the emitted electrons? given, h=6.63×10−34Js,me=9×10−31kg,c=3×108ms−1.
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)
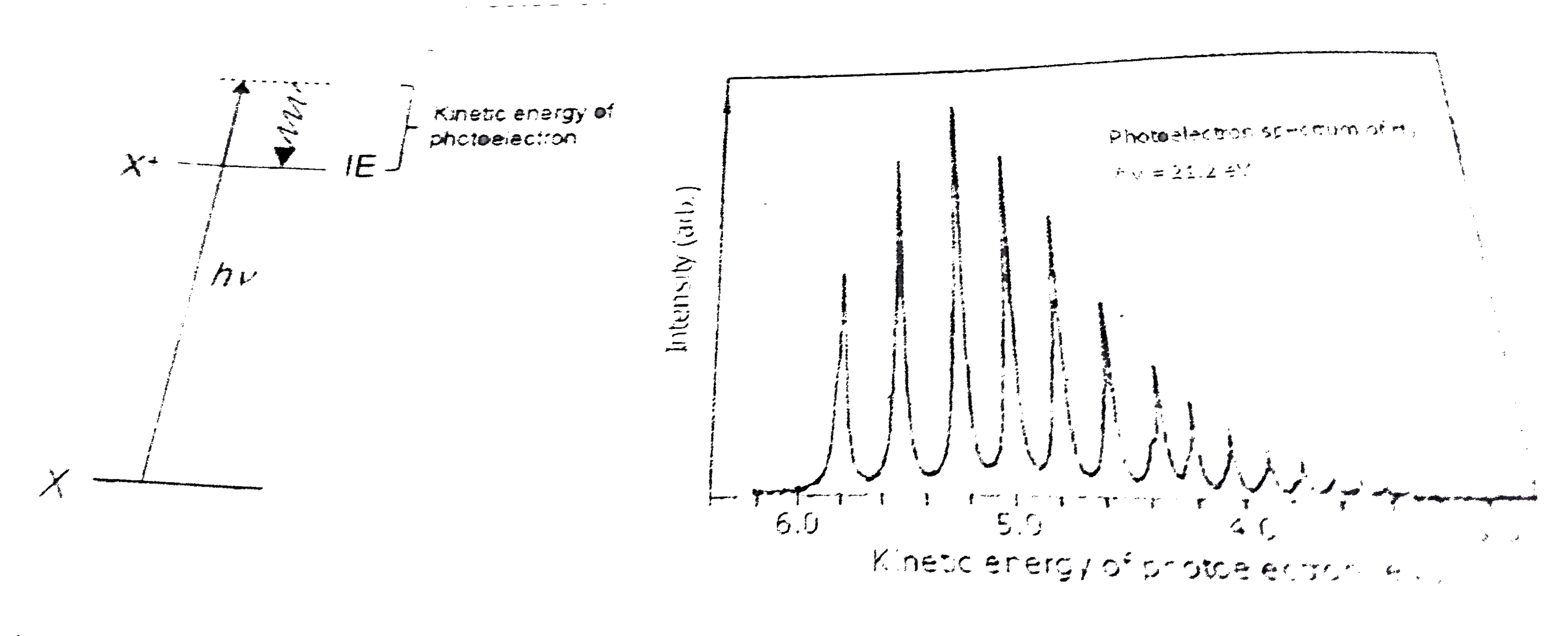
Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Considering an energy cycle, determine––––––––––– the bond energy ED(eV) of H+2 to the first decimal place. If you were unable to determine the values for EB and EC, then use 15.0eV and 5.0eV for EB and EC, respectively.
View SolutionThe work function of cesium metal is 2.14 eV .When light of frequency 6×1014 Hz is incident on the metal surface.phtoemission of electrons occurs. What is the :
(a) maximum kinetic energy of the emitted electrons,
(b) stopping potential , and
(c) maximum speed of the emitted photo - electrons ?
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)

Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Calculate––––––––––– the ionization energy EB(eV) of the hydrogen atom to the first decimal place.
The energy threshold for the generation of two electronically excited hydrogen atoms H∗(n=2) from H2(v=0) has been derived to be 24.9eV by an experiment.
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)
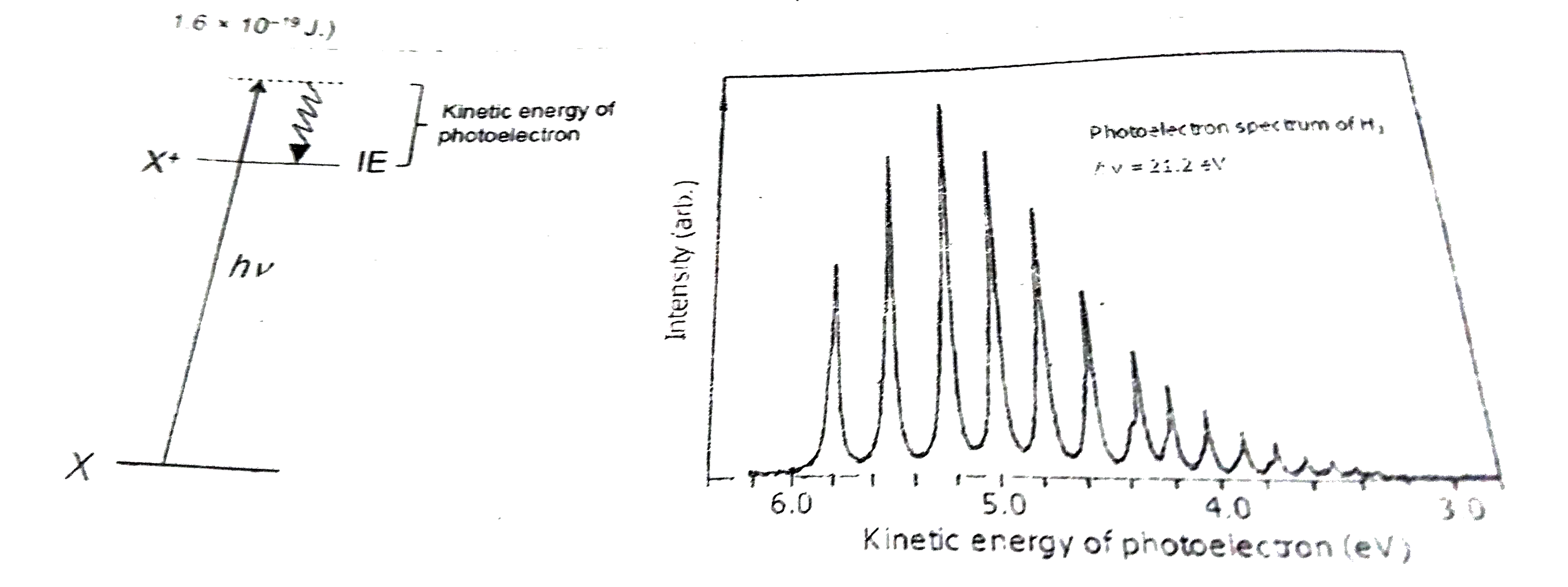
Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Calculate––––––––––– the speed u(ms−1) of the hydrogen atoms generated in the above reaction. H2 is assumed to be at rest. If you were unable to determine the value for EC, then use 5.0eV for EC
View Solution