An ideal gas goes through a cycle consisting of isothermal polytropic and adiabatic lines with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n-fold within the cycle.
The section from p1 V1 To to p2 V2 T0/n is a polytropic process of index α We shall assume that the corresponding specific heat C is + ve.
Related Solutions
An ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies within the cycle.
View SolutionAn ideal gas goes through a cycle consisting of (a) isochoric, adiabatic, and isothermal lines , (b) isobaric, adiabatic, and isothermal lines, with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n-fold within the cycle.
View SolutionFind the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies and the absolute temperature within the cycle. The working substance is an ideal gas with the adiabatic exponent .
View SolutionAn ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies times with tn the cycle then find out its effcincy.
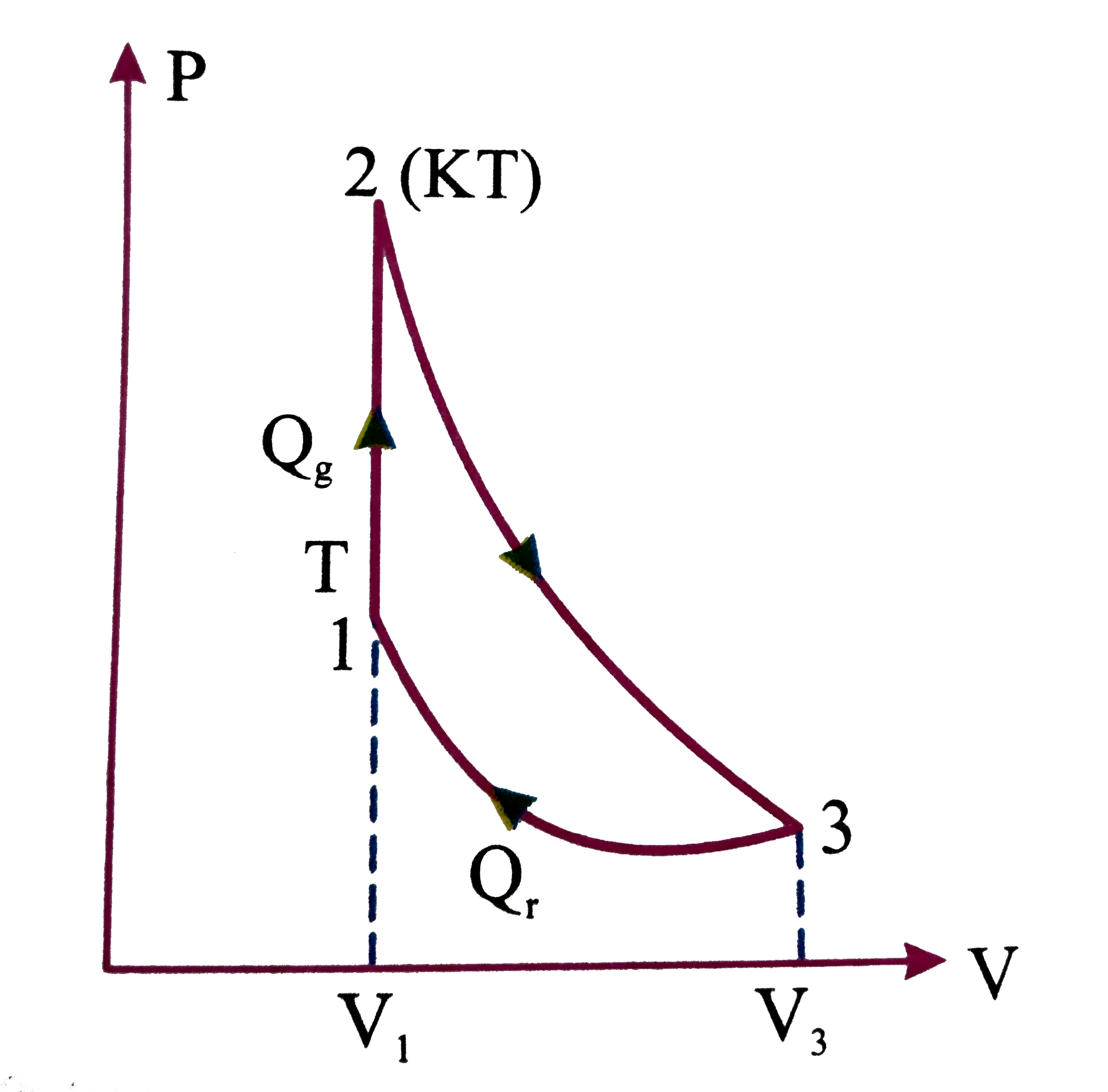
View SolutionAn ideal gas with the adiabatic exponent gamma goes through a cycle (Fig. 2.3) within which the absolute temperature varies tau-fold . Find the efficiency of this cycle. .
View SolutionFind the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies and the absolute temperature within the cycle. The working substance is an ideal gas with the adiabatic exponent .
View SolutionAn ideal gas with the adiabatic exponent y goes through a direct (clockwise) cycle, consisting of adiabatic, isobaric and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas increases n fold.
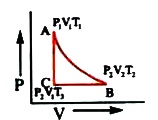
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
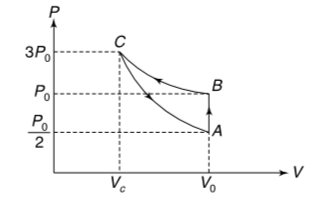
View Solutioncycle is made of three process is iso barie, adiabatic and isothermal. Isothermal process has minimum temperature. Absolute temperature charges by times withing the cycle. Find out the efficiency.
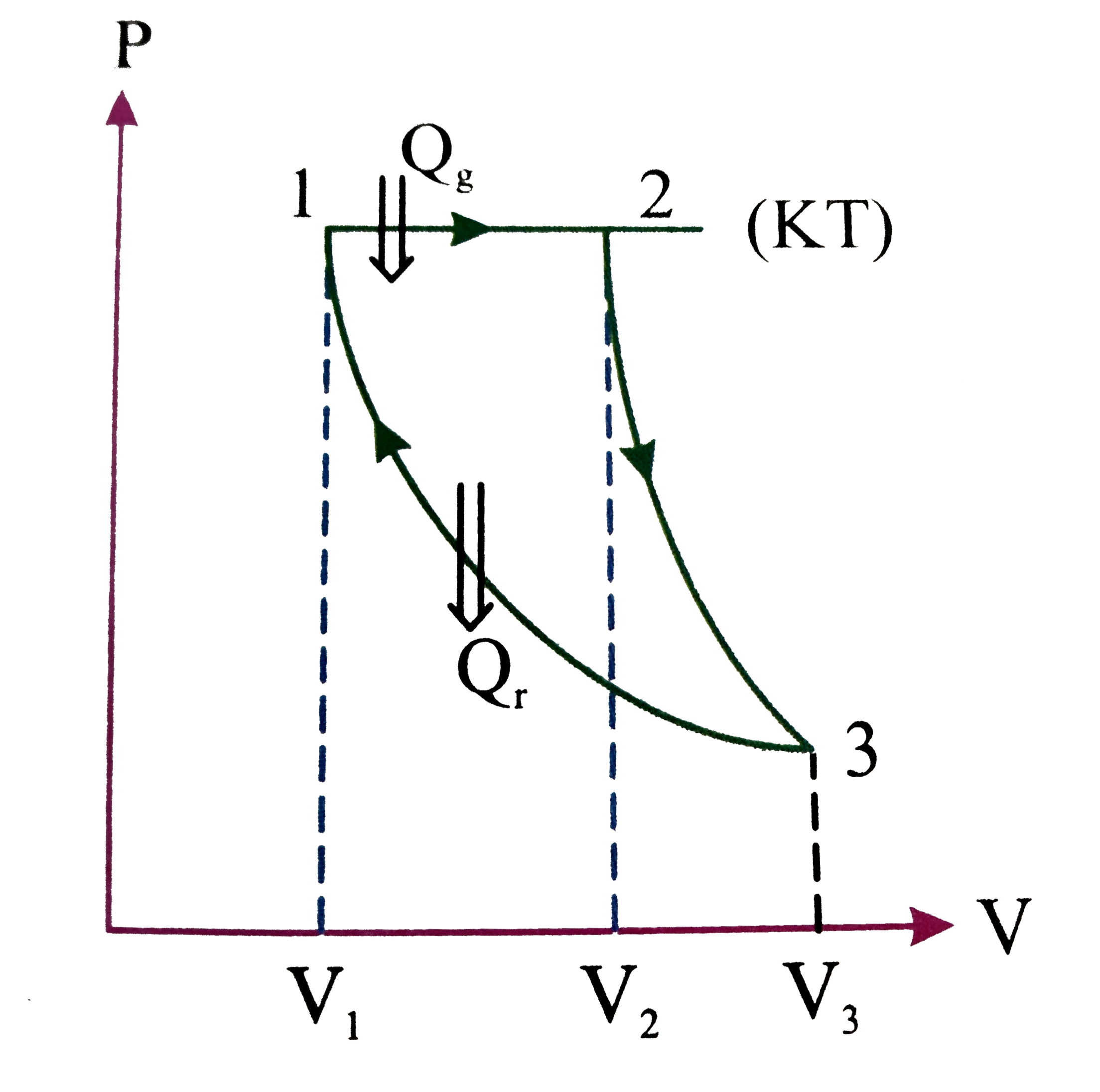
View SolutionAn ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T_1, T_2 and T_3 . Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion. .
View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent .
(a) increased ,
(b) decreases .
View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle. .
View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle. .
View SolutionA working substance goes through a cycle within which the absolute temperature varies n-fold , and the shape of the cycle is shown in (a) Fig.a , (b) Fig. b, where T is the absolute temperature, and S the entropy. Find the efficiency of each cycle. .
View SolutionAn ideal gas with the adiabatic exponent goes through a direct (clockwise) cycle conisting of adiabatic, isobaric, and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas.
(a) increases n-fold ,
(b) decreases n-fold.
View SolutionAn ideal gas undergoes a circular cycle as shown in the figure. Find the ratio of maximum temperature of cycle to minimum temperature of cycle.
View SolutionAn ideal gas undergoes a circular cycle as shown in the figure. Find the ratio of maximum temperature of cycle to minimum temperature of cycle.
View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
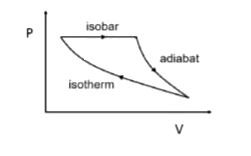
View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )

View SolutionAn ideal gas is taken through cycle 1231 (see figure) and the efficiency of the cycle was found to be 25%. When the same gas goes through the cycle 1341 the efficiency is 10%. Find the efficiency of the cycle 12341.
View Solution