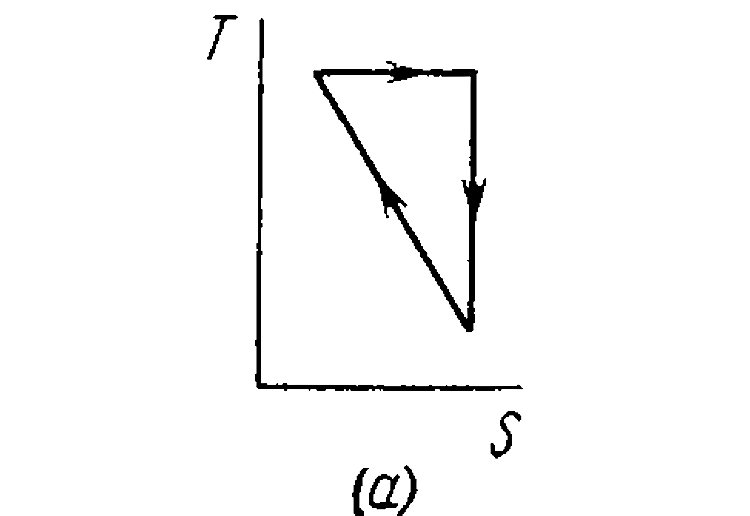
A working substance goes through a cycle within which the absolute temperature varies n−fold, and the shape of the cycle is shown in
(a) Fig.a ,
(b) Fig. b, where T is the absolute temperature, and S the entropy. Find the efficiency of each cycle.
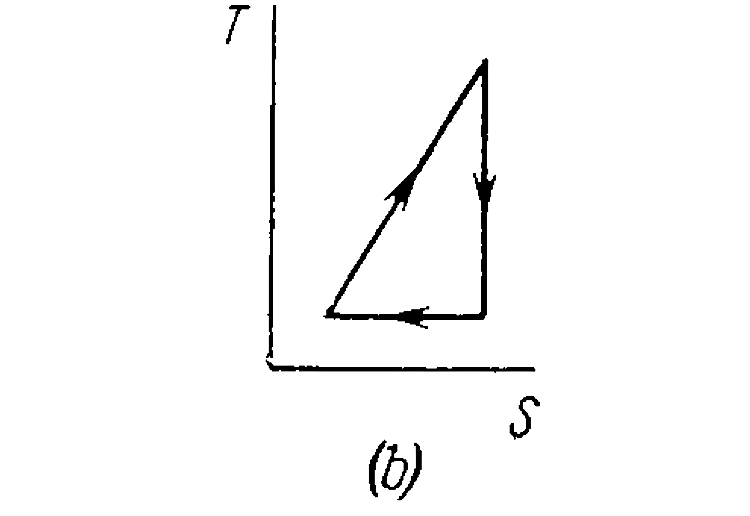 .
.
(a) we have from the definition
Q=∫TdS= area under the curve
Q1=T0(S1−S2)
Q'2=12(T0+T1)(S1−S0)
Thus, using T1=T0n,
η=1−T0+T12T0=1−1+1n2=n−12n
(b) Here Q1=12(S1−S0)(T1+T2)
Q'2=T1(S1−S0)
η=1−2T1T1+T2=T0−T1T0−T1=n−1n+1.
 ,
,
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An ideal gas with the adiabatic exponent γ goes through a cycle (Fig. 2.3) within which the absolute temperature varies τ−fold. Find the efficiency of this cycle.
 .
.
View SolutionAn ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.
View Solution
Knowledge Check
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnKIn a Carnot's cycle, the working substance absorbs heat Q1 at temperature T2. The change of entropy the Carnot's cycle is
AQ1T1BQ2T2CQ1T1+Q2T2DZeroIn a Carnot's cycle, the working substance absorbs heat Q1 at temperature T2. The change of entropy the Carnot's cycle is
AQ1T1BQ2T2CQ1T1+Q2T2DZero
An ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
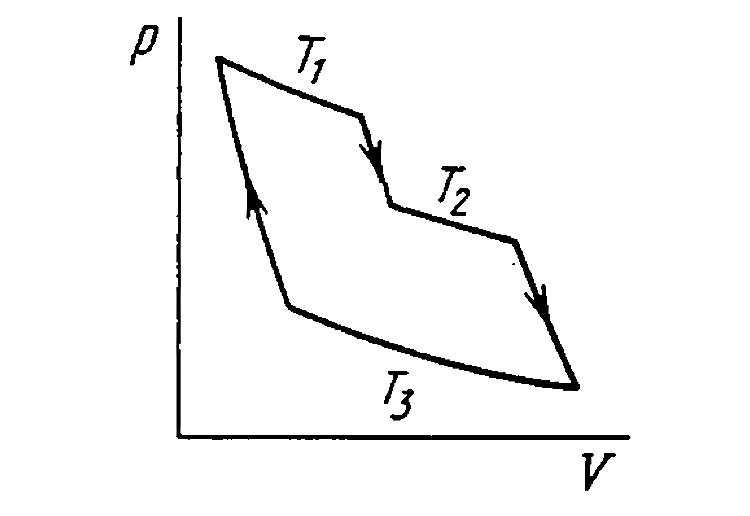
View SolutionAn ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1,T2 and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion.
 .
.
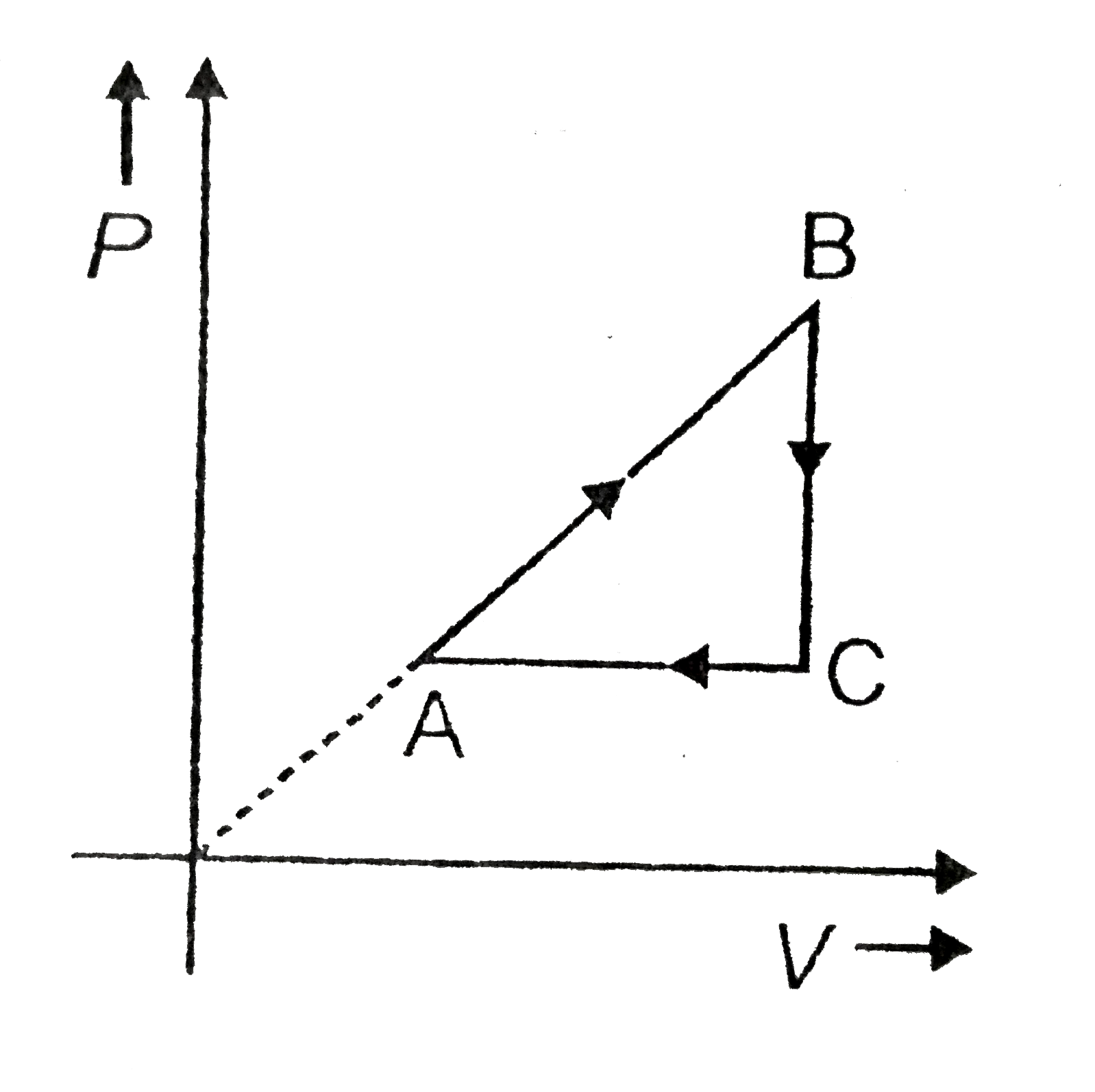
View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle.
 .
.
View SolutionThe specific heat of a metal at low temperatures varies according to S=(45)T3, where T is the absolute temperature, Find the heat energy (in SI unit) needed to rate the temperature of unit mass of the metal from T=1K to T=2K
View SolutionThe specific heat of a metal at low temperature varies according to S=(4/5)T3 where T is the absolute temperature. Find the heat energy needed to raise unit mass of the metal from T = 1 K →T= 2K.
View Solution