Find the entropy increment of one mole of a Van der Waals gas due to the isothermal variation of volume from V1 to V2. The Van der Walls corrections are assumed to be known.
Video Solution
Text Solution
For a Vander Waal gas
(p+aV2)(V−b)=RT
The entropy change along an isotherm can be calculated from
ΔS=∫V2V1(∂S∂V)TdV
If follows from (2.129) that
(∂S∂V)T=(∂p∂T)V=RV−b
Assuming a,b to be known constants.
Thus ΔS=R1nV2−bV1−b.
|
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
The internal pressure loss of 1mol of van der Waals gas over an ideal gas is equal to
AZeroBb2CaV2Db−aRTFor an van der Waals' gas, the term (abV2) represents some
ApressureBenergyCcritical densityDmolar massFor one mole of a van der Waals' gas when b=0 and T=300K, the pVvs1/V plot is shown below. The value of the vander Waals' constant a(atm Lmol−2)
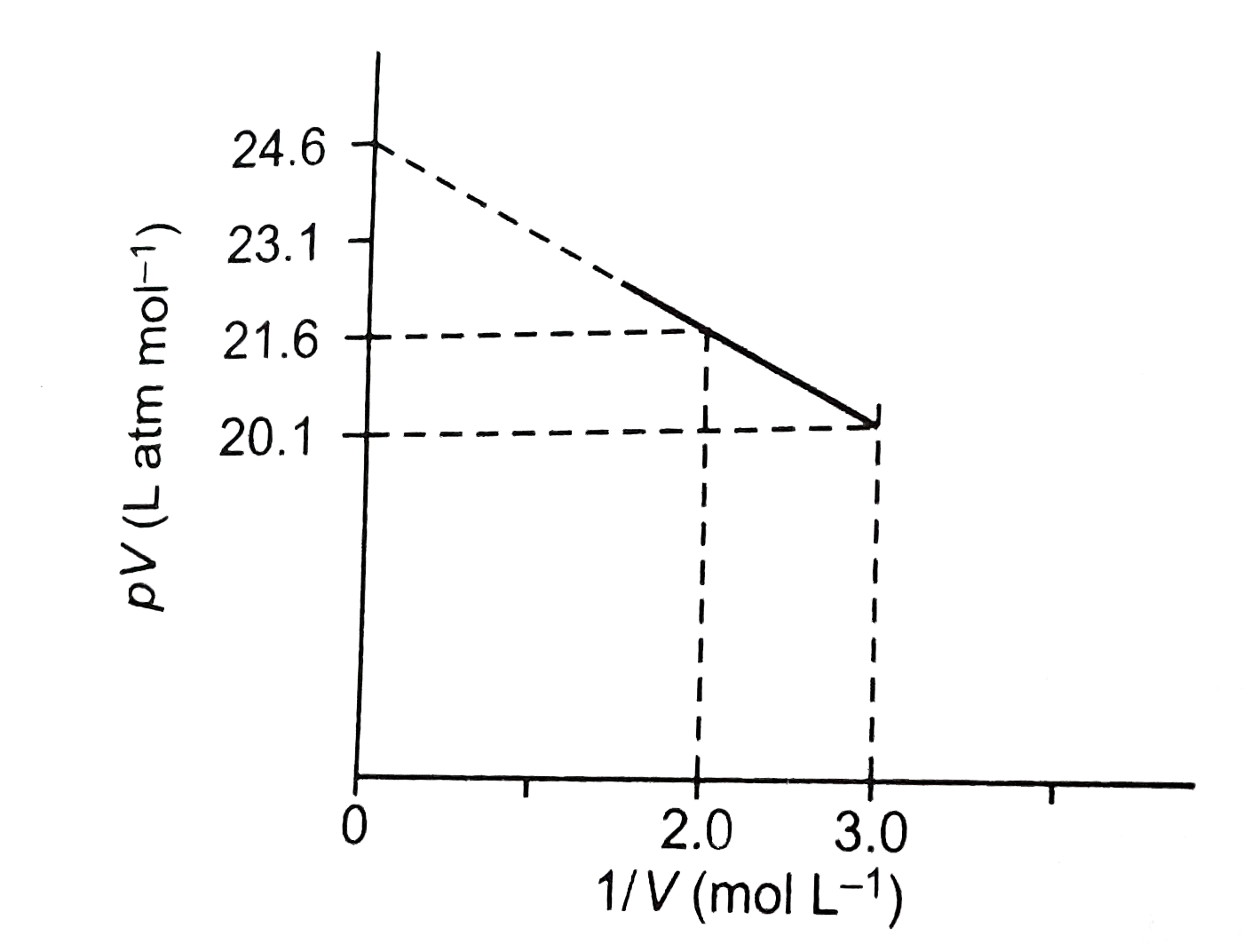 A1B4.5C1.5D3
A1B4.5C1.5D3
Van der Waal's equation at high pressure for 1 mole is
View SolutionThe van der Waals equation for one mole of real gas st low pressure is
View SolutionAt high pressure, the compressibility factor for one mole of van der Waals gas will be
View SolutionThe van der Waals equation for (1/3) rd mole of a gas is
View SolutionFor one mole of a van der Waals gas when b=0 and T=30K the PVvs1/V plot is shown below The value of the van Waals constant a (atm litre2mol−2) is
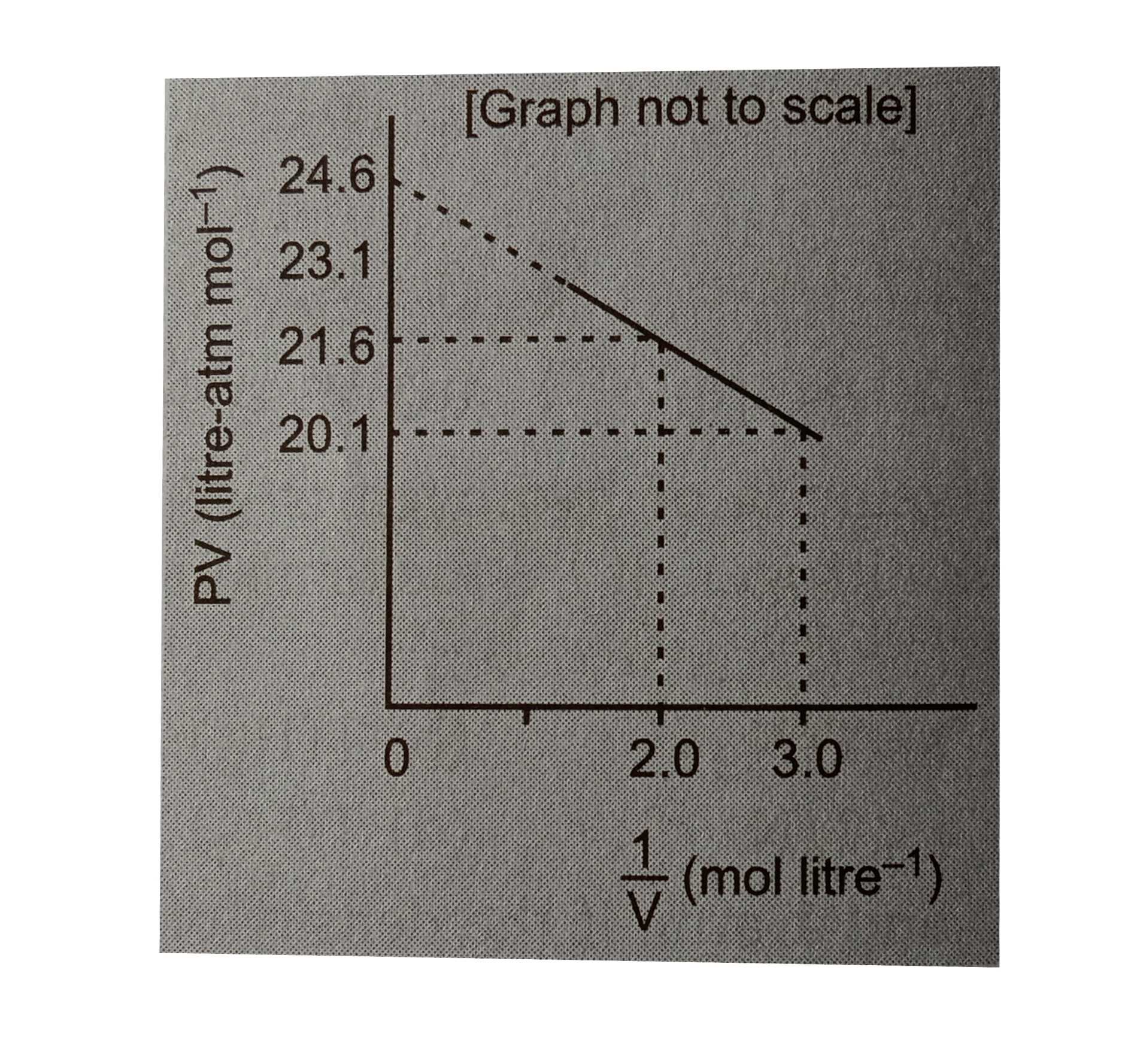 .
.
View Solution
