A uniform ladder of length 13m and weighing 250N is placed against a smooth vertical wall with its lower end 5m from the wall. The coefficient of friction between the ladder and floor is 0.3. Show that the ladder will remain in equilibrium in this position. What is the frictional force acting on the ladder at the point of contact between the ladder and the floor?
Since the ladder is placed against a smooth vertical wall therefore there will be no friction at the point of contact between the ladder and wall. Resolving all the force horizontally and vertically. ∑H = 0 Fr – R2 = 0 ...i ∑V = 0 R1 – 250 ...ii From the geometry of the figure BC = 12m Taking moment about point B R1 × 5 – Fr × 12 – 250 × 2.5 = 0 Fr = 52NFor equilibrium of the ladder Maximum force of friction available at the point of contact between the ladder and the floor = µR = 0.3 × 250 = 75N Thus we see that the amount of the force of friction available at the point of contact 75N is more than force of friction required for equilibrium 52N. Therefore the ladder will remain in equilibrium in this position.
Related Solutions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionIf a ladder weighing 250N is placed against a smooting vertical wall and if coefficent of friction between it a floor is 0.3, then what is the maximum force of friction available at the point of confact between the ladder a the floor.
View SolutionA uniform ladder is standing against a vertical smooth wall, resting on a horizontal floor. The ladder makes an angle of 45^(@) with the floor when its lower end is about to slip. What is the value of the coefficient of friction between the ladder and the floor?
View SolutionIf a ladder weighting is placed against a smooth vertical wall having coefficient of friction between it and floor 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor?
View SolutionA 13 m ladder is placed against a smooth vertical wall with its lower end 5 m from the wall. What should be the minimum coefficient of friction between the ladder and the floor so that it remains in equilibrium?
View SolutionA ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle with the horizontal floor. The coefficient of friction between the wall and the ladder is and that between the floor and the ladder is the normal reaction of the wall on the ladder is and that of the floor is if the ladder is about to slip. than
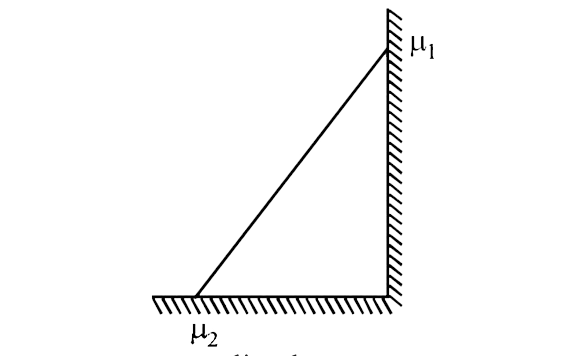
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle theta with the horizontal floor. The coefficient of friction between the wall and the ladder is mu_1 and that between the floor and the ladder is mu_2. the normal reaction of the wall on the ladder is N_1 and that of the floor is N_2. if the ladder is about to slip. than
View SolutionIf a ladder weighting 250 N in placed a smooth vartical wall having coefficient of friction between it and floor 03, then what is the maximum force of fraction available at the point of contact between the ladder and the floor?
View SolutionA person of mass 80 kg is standing on the top of a 18 kg ladder of length 6 m. Upper end of the ladder rests on a smooth vertical wall and the lower end is on the ground 3 m away from the vertical wall. What should be the minimum coefficient of friction between the floor and the ladder so that the system remains in equilibrium ?
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View SolutionA ladder of length and mass is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is . The angle at which the ladder will stay in equilibrium is
View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is mu . The angle theta at which the ladder will stay in equilibrium is
View SolutionA uniform ladder of length rests against a smooth, vertical wall (figure). If the mass of the ladder is and the the coefficient of static friction between the ladder and the ground is and the minimum angle at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
View Solution5 m लम्बाई व 100 kg द्रव्यमान की एक समरूप सीढ़ी ऊर्ध्वाधर चिकनी दीवार व खुरदरी क्षैतिज सतह के मध्य साम्यावस्था में है। इस साम्यावस्था के लिए फर्श व सीढ़ी के मध्य न्यूनतम घर्षण गुणांक ज्ञात करो।
View SolutionA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction and its upper end against a smooth vertical wall. If is the inclination of the ladder with the wall, then is equal to
View SolutionA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction and its upper end against a smooth vertical wall. If is the inclination of the ladder with the wall, then is equal to
View SolutionA ladder of mass 30 kg and length 5 m is kept leaning against a vertical smooth wall. A man of mass 60 kg climbed up the length of the ladder. If the coefficient of friction between the floor and the ladder is 0.5, what should be the maximum distance of the foot of the ladder from the wall to avoid slipping?
View SolutionA ladder weighing 250 N is placed against the Shirolob wall. The other end of it is on the ground. If the friction for ground and ladder is 0.3, find the maximum possible friction between ground and ladder.
View Solution