A uniform ladder of length l rests against a smooth, vertical wall (figure). If the mass of the ladder is m and the the coefficient of static friction between the ladder and the ground is μs=0.375 and the minimum angle θmin at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
Applying the first condition for equilinrium to the ladder, we have
(1) ΣFx=fs−P=0
(2) ΣFy=n−mg=0
The first equation tells us that P=f0. From the second equation we see that n=mg. Furthermore, when the ladder is on the verge of slipping, the force of friction must be a mximum, which is given by fc,max=μsn=μsmg.
The find θmin, we must use the second condition for equilibrium. When we take the torque about an axis through the origin O at the bottom of the ladder, we have
Στ0=Plsinθ−(mg)l2cosθ=0
This expression gives
tanθmin=mg2P=mg2μsmg=12μs=1.25
θmin=53∘.
Any body experiencing zero net force & zero torque about C.M is raid to be in equilibrium.
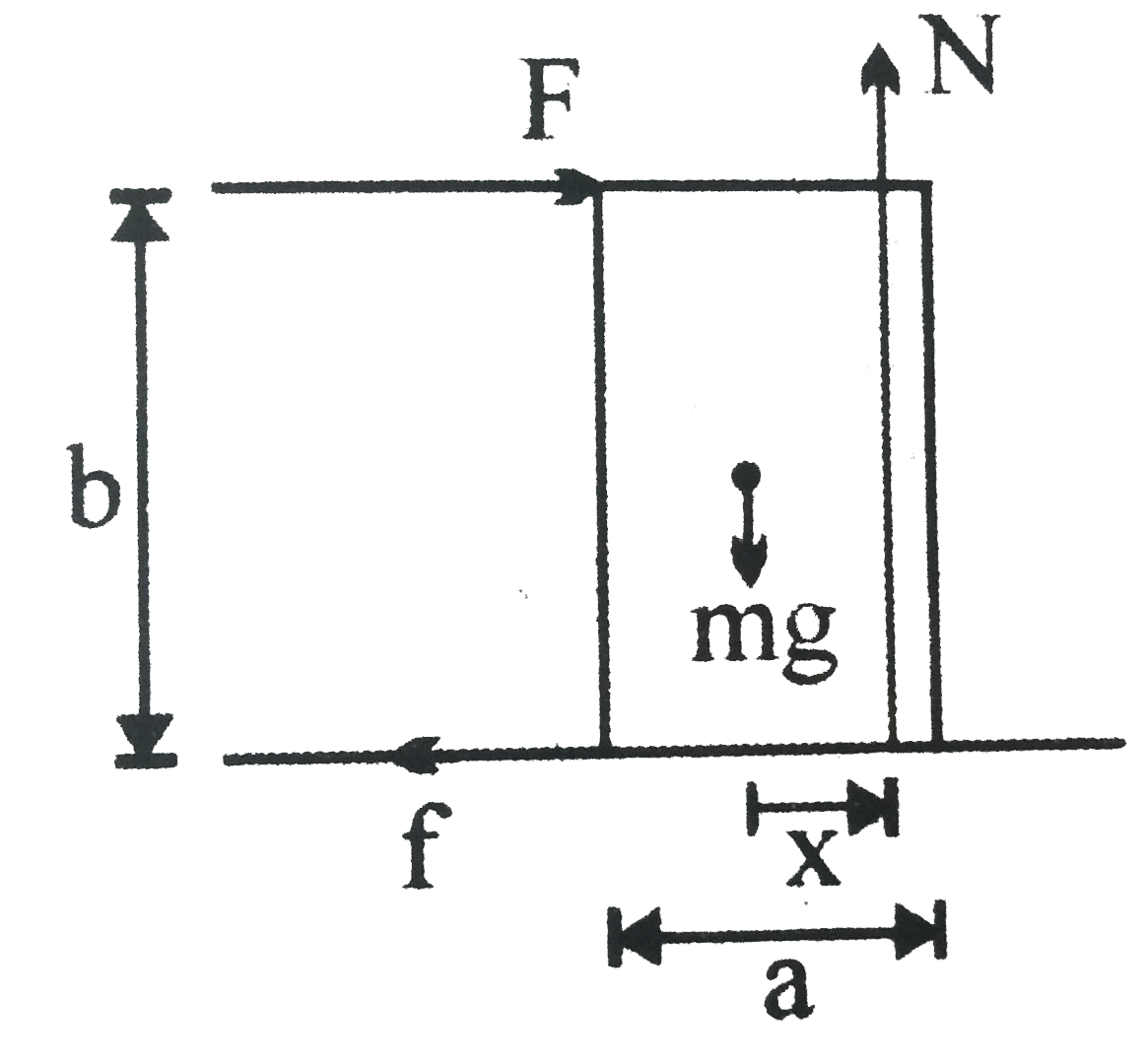
F12+f(1)2−Nx=0
N=mg,F=f
x=FbN=Fbmg
but x<a2
for not toppling a2>Fbmg or a2b>Fmg
assuming F<μmg.
Similar Questions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA ladder of length 50 m rests against a vertical wall, at a height of 30 m from the ground. Find the inclination of the ladder with the horizontal. Also find the distance between the foot of the ladder and the wall.
View Solution
Knowledge Check
A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of theseA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
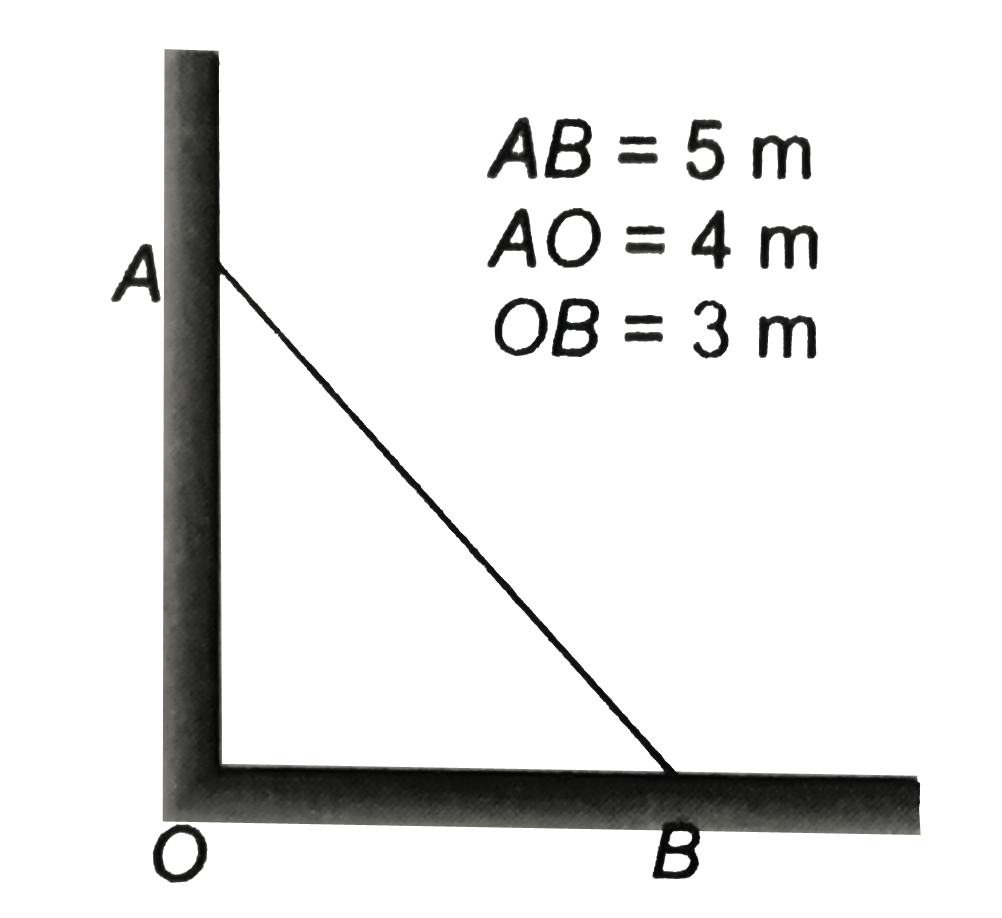 Aμ=12Bμ=14Cμ=38Dμ=58
Aμ=12Bμ=14Cμ=38Dμ=58A uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
How far along the ladder can the man climb before the ladder starts to slip?A3mB5mC2.7mD1.25m
A ladder 10m long rests against a vertical wall. If the foot of the ladder is 6m away from the wall and the ladder just reaches the top of the wall, how high is the wall?
View SolutionA ladder rests on the floor of a room, leaning agains a wall. If the coefficient of static friction between the ladder the floor is μf and that between ladder and is μw, what is the minimum angle θ that the ladder can make with the floor if the ladder is not to slip? Assume that the mass of the ladder is distributed uniformly.

View SolutionA uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
What is the maximum frictional force that the ground can exert on the ladder at its lower end?
View SolutionIf a ladder is not in balance against a smooth vertical wall, then it can be made in balance by :-
View SolutionA uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
What is the actual frictional force when the man has climbed 1.0m along the ladder?
View Solution

