A ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
40 N
50 N
60 N
70 N
The correct Answer is:C
To find the maximum force of friction available at the point of contact between the ladder and the floor, we can follow these steps:
Step 1: Understand the Problem
We have a ladder weighing 300 N placed against a smooth vertical wall. The coefficient of friction between the ladder and the floor is given as 0.2. We need to determine the maximum force of friction at the point of contact between the ladder and the floor.
Step 2: Identify the Forces Acting on the Ladder
The forces acting on the ladder are:
- The weight of the ladder (W = 300 N) acting downwards.
- The normal reaction force (R) acting upwards at the point of contact with the floor.
- The frictional force (F_friction) acting horizontally at the base of the ladder, opposing any motion.
Step 3: Apply the Formula for Maximum Frictional Force
The maximum force of friction (F_friction) can be calculated using the formula:
Ffriction=μ⋅R
where:
- μ is the coefficient of friction (0.2 in this case).
- R is the normal reaction force.
Step 4: Determine the Normal Reaction Force
In this scenario, since the ladder is in equilibrium and there are no vertical movements, the normal reaction force (R) is equal to the weight of the ladder:
R=W=300N
Step 5: Calculate the Maximum Frictional Force
Now, we can substitute the values into the friction formula:
Ffriction=μ⋅R=0.2⋅300N
Ffriction=60N
Conclusion
The maximum force of friction available at the point of contact between the ladder and the floor is 60 N.
---
We have a ladder weighing 300 N placed against a smooth vertical wall. The coefficient of friction between the ladder and the floor is given as 0.2. We need to determine the maximum force of friction at the point of contact between the ladder and the floor.
The forces acting on the ladder are:
- The weight of the ladder (W = 300 N) acting downwards.
- The normal reaction force (R) acting upwards at the point of contact with the floor.
- The frictional force (F_friction) acting horizontally at the base of the ladder, opposing any motion.
The maximum force of friction (F_friction) can be calculated using the formula:
Ffriction=μ⋅R
where:
- μ is the coefficient of friction (0.2 in this case).
- R is the normal reaction force.
In this scenario, since the ladder is in equilibrium and there are no vertical movements, the normal reaction force (R) is equal to the weight of the ladder:
R=W=300N
Now, we can substitute the values into the friction formula:
Ffriction=μ⋅R=0.2⋅300N
Ffriction=60N
The maximum force of friction available at the point of contact between the ladder and the floor is 60 N.
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS Book:MARVEL PUBLICATIONChapter:FRICTIONAL IN SOLIDS AND LIQUIDS Exercise:TEST YOUR GRASP
Explore 10 Videos
- FORCE, WORK AND TORQUEBook:MARVEL PUBLICATIONChapter:FORCE, WORK AND TORQUEExercise:TEST YOUR GRASP
Explore 10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT Book:MARVEL PUBLICATIONChapter:MAGNETIC EFFECT OF ELECTRIC CURRENT Exercise:TEST YOUR GRASP
Explore 10 Videos
Similar Questions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
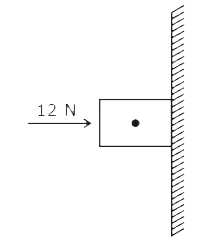
View Solution
Knowledge Check
If a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
A75NB50NC35ND25NIf a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
A75NB50NC35ND25NIf a ladder weighting 250N in placed a smooth vartical wall having coefficient of friction between it and floor 03, then what is the maximum force of fraction available at the point of contact between the ladder and the floor?
A75NB50NC35ND25N
The coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :

View Solution

