A heavy ring of mass m is clamped on the periphery a light circular disc. A small particle having equal mass is clamped at the centre of the disc . The system rotated in such a way that the centre moves in a circular of radius r with a uniform speed v. We conclude that a external forcea mv2/r must be acting on the central particleb 2mv2/r must be acting on the central particlec 2mv2/r must be acting on the systemd 2mv2/r must be acting on the ring.
c 2mv2/r must be acting on the systemExplanation: Since the heavy ring and the small particle have equal masses the center of mass of the system will be at r/2 from the ring. Hence the force acting on the system =mv²/r/2 = 2mv²/r.
Related Solutions
A heavy ring fo mass m is clamped on the periphery of a light circular disc.A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre of mass moves in a circle of radius r with a uniform speed v. We conclude that an external forec :
View SolutionA heavy ring fo mass m is clamped on the periphery of a light circular disc.A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre of mass moves in a circle of radius r with a uniform speed v. We conclude that an external force :
View SolutionA heavy ring fo mass m is clamped on the periphery of a light circular disc.A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre of mass moves in a circle of radius r with a uniform speed v. We conclude that an external force :
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is . Find the centre of mass of the remaining part of the disc.

View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is . Find the centre of mass of the remaining part of the disc.

View SolutionFrom a uniform circular dis of radius R , a circular dis of radius R//6 and having centre at a distance R//2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of radius R of same thickness and density. The peripheries of the two disc touch each other. The centre of mass of the system from centre of big disc is
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFrom the circular disc of radius two small discs of radius R are cut off. The centre of mass of the new structure will be at
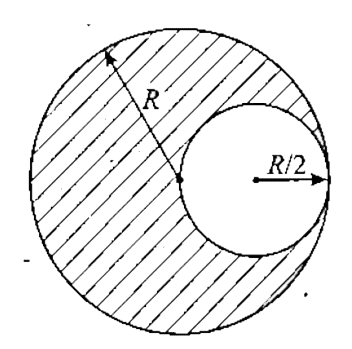
View SolutionFrom the circular disc of radius two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionIf a square of side R/2 is removed from a uniform circular disc of radius R as shown in the figure, the shift in centre of mass is
View SolutionIf a square of side R/2 is removed from a uniform circular disc of radius R as shown in the figure, the shift in centre of mass is:

View SolutionFrom a uniform disc of radius , a circular section of radius is cut out. The centre of the hole is at from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFrom a uniform disc of radius , a circular section of radius is cut out. The centre of the hole is at from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA uniform disc of diameter R//2 is put over another uniform disc of diameter R of same thickness and density. The peripheries of the two disc touch each other. The centre of mass of the system from centre of big disc is
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of diameter R of same thickness and density. The peripheries of the two disc touch each other. The centre of mass of the system from centre of big disc is
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of diameter R of same thickness and density. The peripheries of the two discs touch each other. The centre of mass of the system from centre of big disc is
View Solution