Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

The disc will be like the one shown below

The axis of symmetry of the above body will pass through the centres of the complete disc and the hole.
The centre of mass of the remaining part of disc will tie on the aixs of symmetry and one can easily guess that it will be to the left of O. Let it be at O at a distance x from the centre O.
Now , the initial complete disc can be regarded as a two component system, with one component the circular disc of radius R/2 and the remaining disc. The complete disc can be shown like the one below.

Let O be the origin. So we can assume that there are two particles of masses m1 and m2 kept at O and O' respectively. The centre of mass of a two particle, we can write
xcm=m1x1+m2x2m1+m2
Now, xcm=0 (∵O is at origin)
The masses can be taken proportional to the area. the actual value of masses does not really matter.
So, m1∝π[R2−(R(2)2]
and m2∝π[(R2)2]
So, if m2=m, m1=3m. Substituting the values, we obtain
0=3m×x1+m×R2m1+m2
⇒x1=−R6
The negative sign signifies that O is located to left of O.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
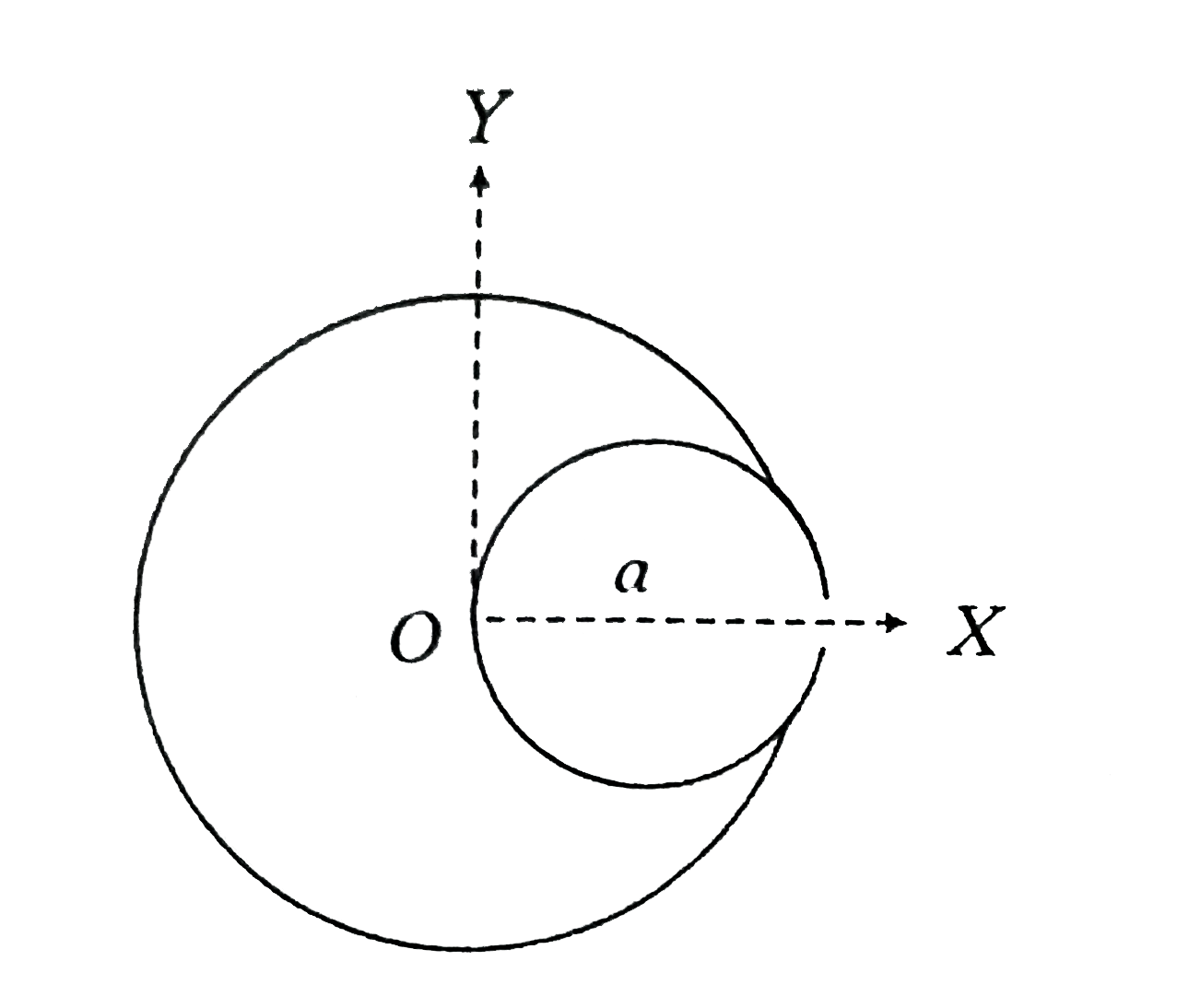
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View Solution
