A cone of radius R and height H is hanging inside a liquid of density ρ by means of a string as shown in the figure. The force due to the liquid acting on the slant surface of the cone is Neglect atmosphere pressure A πρgHR2 B πρHR2C 4/3πρgHR2 D 2/3πρgHR2
The correct Answer is:Option D
Correct Option D 2/3πρgHR2 Explanation:Buoyant force = sum of all forces acting on the body = force acting on the slant surface + force acting on the bottom surface
Related Solutions
A cone of radius .R. and height H is immersed fully inside a liquid of density by means of a string. The force due to the liquid acting on the slant surface of the cone is (neglect atmospheric c pressure)
View SolutionA cone of radius and height , is hanging inside a liquid of density by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
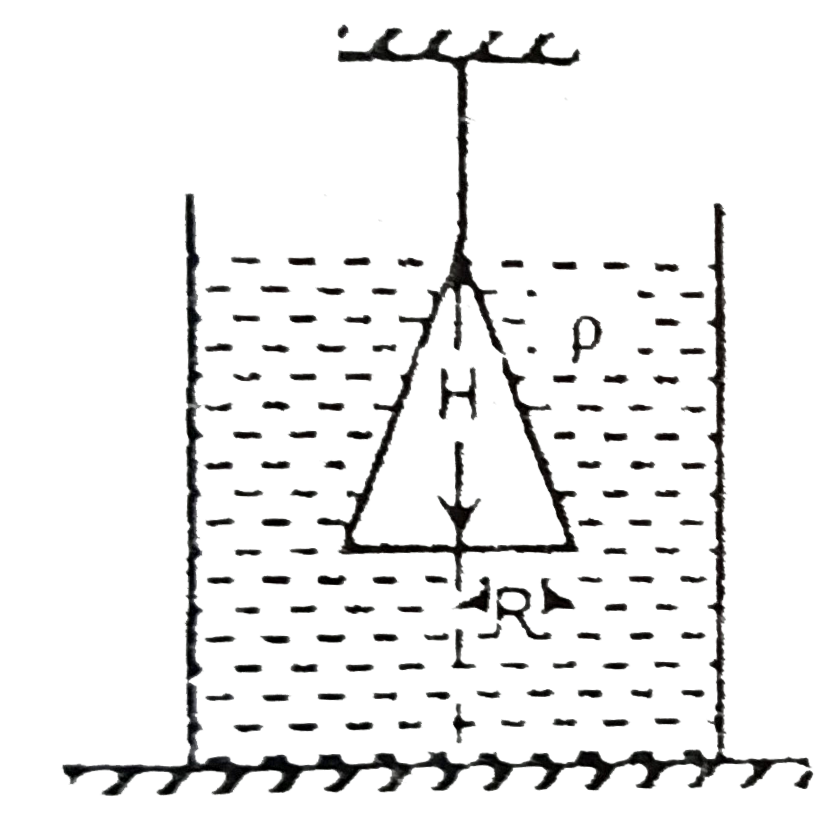
View SolutionA cone of radius R and height H , is hanging inside a liquid of density rho by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
View SolutionThe cone of radius and height is hanging inside a liquid of density by means of a string a shwon in the figure.

View SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.
View SolutionA cone of radius R and height H, density rho K is suspended from a string inside a liquid, as shown in the figure. The force due to the fluid acting on the oblique surface of the cone is:
View SolutionA cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)
View SolutionA solid cone of height H and base radius floats in a liquid of density . It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is ( atmospheric pressure)
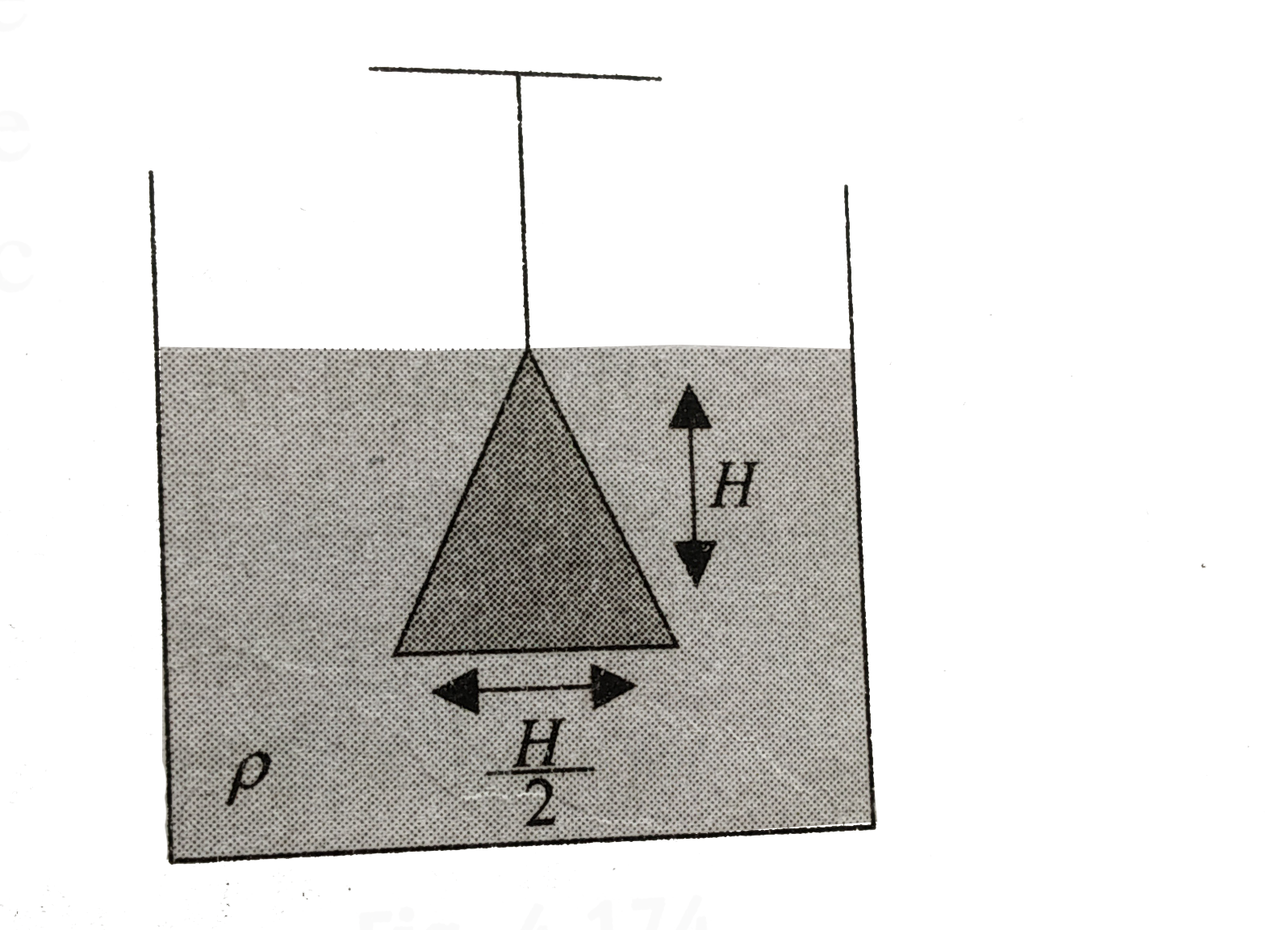
View SolutionA solid cone of height H and base radius H/2 floats in a liquid of density rho . It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is ( P_(0) = atmospheric pressure)
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d( ltrho , density of water). (a) Find tension in the string. (b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p_(0) .
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is V . In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d (lt rho , density of water) Then tension in the string is
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is and the volume of the cone is . In equilibrium the base of the cone is at a depth below the water surface. Density of wood is , density of water) Then tension in the string is
View SolutionThe height of a cone is 3 m and its radius is 4 m. Find the slant height and slant surface of the cone.
View Solutionएक शंकु की त्रिज्या और तिरछी ऊँचाई है, का कुल पृष्ठीय क्षेत्रफल होगा
View SolutionA solid cone of uniform density and height 2R and base radius R has a conical portion scooped out form its base with the same base radius but height R as shown in the figure. The solid cone is floating in a liquid of density rho with vertex A touching the fluid surface . If atomospheric pressure is P_0 the force acting on the surface BCD due to liquid is
View SolutionThe radius and the slant height of a cone are in the ratio of 4:7. If its curved surface area is 792 cm^(2) . The radius of cone is
View SolutionThe ratio of the radius and the slant height of a cone is 4:7 and the area of its curved surface is .Find the radius of the cone.
View SolutionHeight of cone, if slant height is L and and radius is R
View SolutionDensity|| Relative Density|| Specific Gravity|| Pressure|| Force Due to Pressure|| Variation OF Pressure|| Force on Surface Inside Liquid
View SolutionDensity|| Relative Density|| Specific Gravity|| Pressure|| Force Due to Pressure|| Variation OF Pressure|| Force on Surface Inside Liquid
View Solution