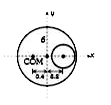
A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
0.4m
2.4cm
1.8cm
1.2cm
The correct Answer is:A
Big disc
A=π(6)2
x1=0,y1=0
Small disc a=π(2)2
x2=3.2,y2=0
xCOM=Ax1−ax1A−a=π(6)2×0−π(2)2×3.2π(62−22)=−0.4cm
Similar Questions
Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius alpha/2 is cut from disc of radius a.
View SolutionA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is
View SolutionA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
View SolutionA circular hole of radius 1 cm is cut by a disc of radius 6 cm. The center of the hole is 3 cm from the center of the disc. Then the distance of the center of mass of the rest of the disc from the center of the disc is:
View Solution