From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
R4π−2
R2π
Rπ−2
R2π−2
The correct Answer is:A
To solve the problem of finding the distance of the center of mass of the remaining portion of a circular disc after cutting out a square, we can follow these steps:
Step 1: Understand the Geometry
We have a circular disc of radius R and a square is cut out such that the diagonal of the square is equal to the radius R of the disc.
Step 2: Determine the Side Length of the Square
The diagonal d of the square is given by:
d=R
Using the relationship between the side length a of the square and its diagonal:
d=a√2⟹a=R√2
Step 3: Calculate the Area of the Square
The area As of the square can be calculated as:
As=a2=(R√2)2=R22
Step 4: Calculate the Mass of the Disc and the Square
Assuming the density of the material is ρ:
- The mass Md of the disc is:
Md=ρ⋅Area of the disc=ρ⋅πR2
- The mass Ms of the square is:
Ms=ρ⋅As=ρ⋅R22
Step 5: Set Up the Coordinate System
Assume the center of the disc is at the origin (0,0). The center of the square, which is cut out, will be at:
(R2√2,0)
Step 6: Calculate the Center of Mass of the Remaining Portion
Using the formula for the center of mass of a system of particles:
xcm=Md⋅xd−Ms⋅xsMd−Ms
Substituting the values:
- xd=0 (center of the disc)
- xs=R2√2
We have:
xcm=(ρπR2)⋅0−(ρR22)⋅(R2√2)Md−Ms
=−(ρR34√2)ρπR2−ρR22
Step 7: Simplify the Expression
The denominator simplifies to:
ρR2(π−12)
Thus, we have:
xcm=−R34√2R2(π−12)=−R4√2(π−12)
Step 8: Final Result
The distance of the center of mass of the remaining portion from the center of the disc is:
Distance=R4√2(π−12)
We have a circular disc of radius R and a square is cut out such that the diagonal of the square is equal to the radius R of the disc.
The diagonal d of the square is given by:
d=R
Using the relationship between the side length a of the square and its diagonal:
d=a√2⟹a=R√2
The area As of the square can be calculated as:
As=a2=(R√2)2=R22
Assuming the density of the material is ρ:
- The mass Md of the disc is:
Md=ρ⋅Area of the disc=ρ⋅πR2
- The mass Ms of the square is:
Ms=ρ⋅As=ρ⋅R22
Assume the center of the disc is at the origin (0,0). The center of the square, which is cut out, will be at:
(R2√2,0)
Using the formula for the center of mass of a system of particles:
xcm=Md⋅xd−Ms⋅xsMd−Ms
Substituting the values:
- xd=0 (center of the disc)
- xs=R2√2
xcm=(ρπR2)⋅0−(ρR22)⋅(R2√2)Md−Ms
=−(ρR34√2)ρπR2−ρR22
The denominator simplifies to:
ρR2(π−12)
Thus, we have:
xcm=−R34√2R2(π−12)=−R4√2(π−12)
The distance of the center of mass of the remaining portion from the center of the disc is:
Distance=R4√2(π−12)
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Assertion and reason
Explore 21 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Match the coloumns
Explore 9 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Check points
Explore 50 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
From a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View Solution
Knowledge Check
From the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
 AˆiR5+ˆjR5B(b) −ˆiR5+ˆjR5C(c) −ˆiR5−ˆjR5D(d) None of the above
AˆiR5+ˆjR5B(b) −ˆiR5+ˆjR5C(c) −ˆiR5−ˆjR5D(d) None of the aboveA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
A13B12C16D14From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2
From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
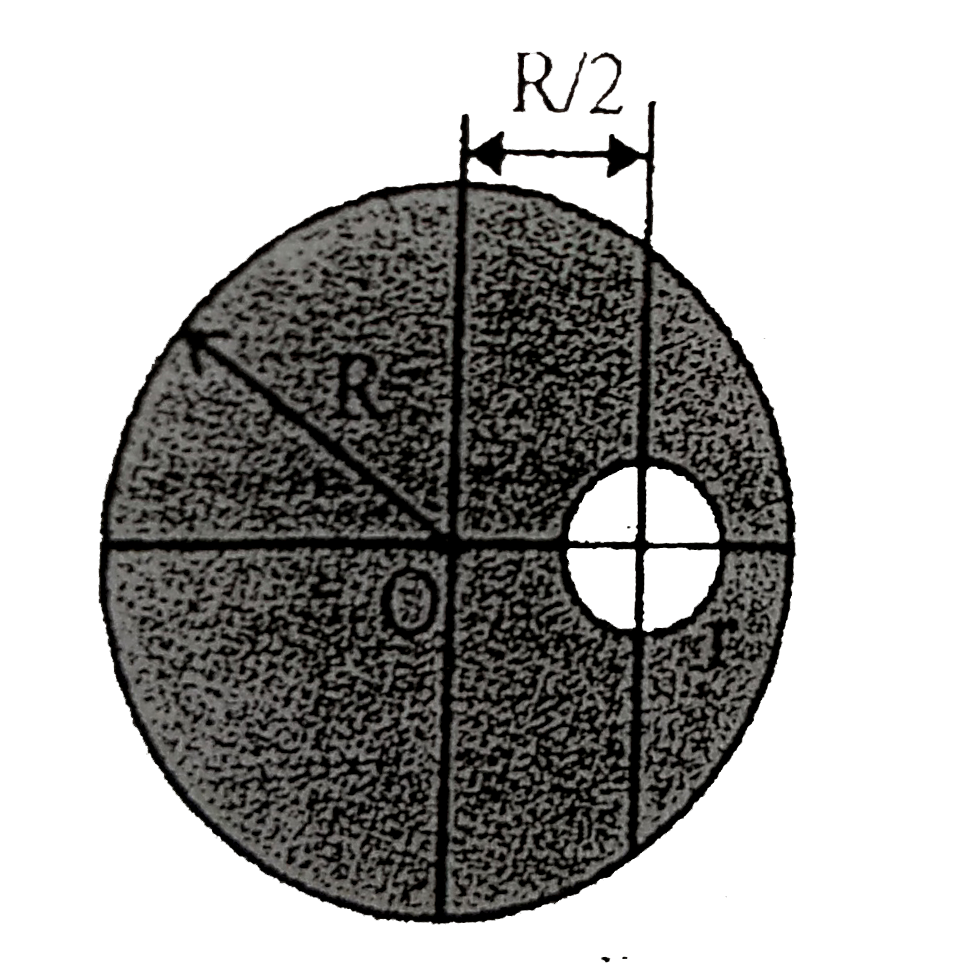
View Solution