From a circular disc of radius R a square is cut out with a radius as its diagonal . The distane of the centre of mass of the remainder from the centre of the disc is
R4π−2
R2π
Rπ−2
R2π−2
The correct Answer is:A
A1(C1)=A2(C2)
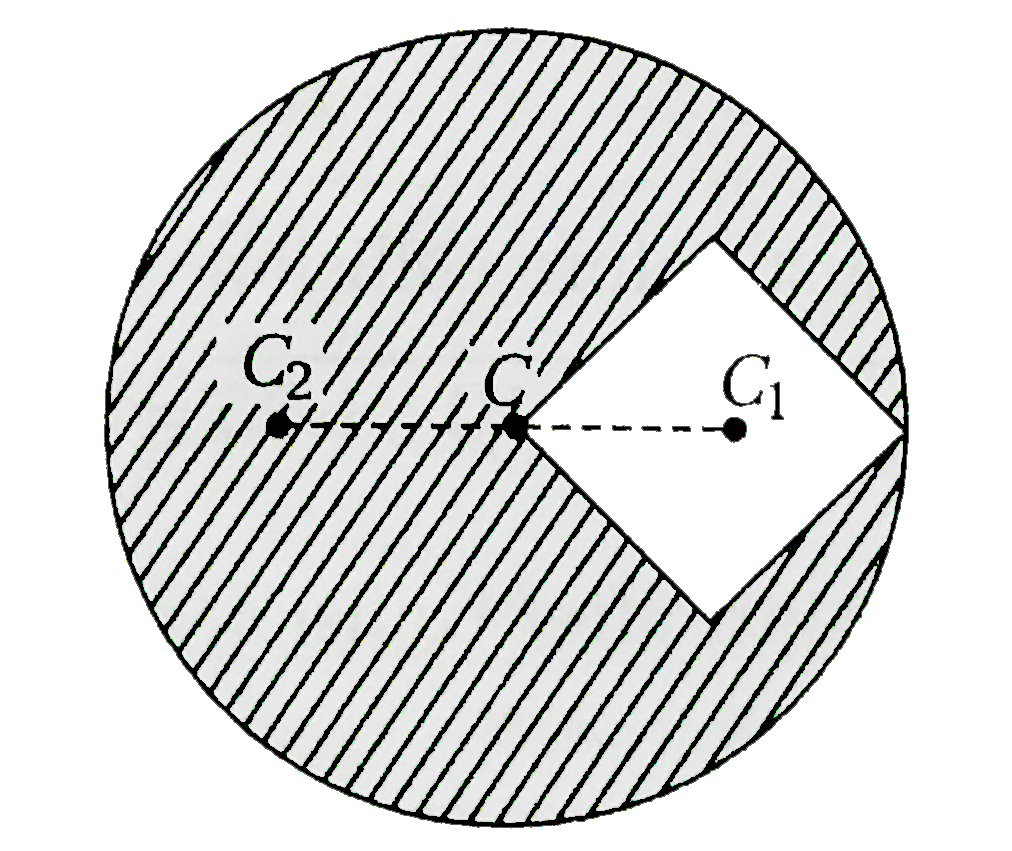
side of square will be R√2
∴C2=A1A2⎛⎜
⎜
⎜⎝C1=(R√2)2πR2−(R/√2)2(R2)=R4π−2
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Assertion and reason
Explore 21 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Match the coloumns
Explore 9 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Check points
Explore 50 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionFrom a circular disc of radius R a square is cut out with a radius as its diagonal . The distane of the centre of mass of the remainder from the centre of the disc is
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View Solution

