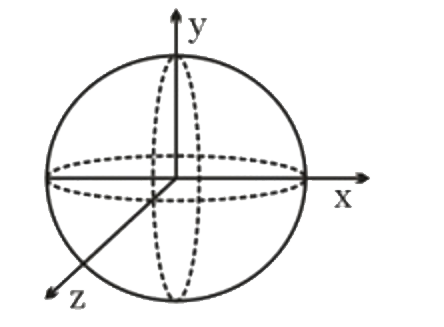
Three rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is
(π2,13)
(π2,23)
(π,13)
(π,23)
The correct Answer is:D
2πR=2π∴R=1
yCM=m×0+m×1+m×1m+m+m=23
x9CM)=m(π)+m(0)+m(2π)m+m+m=π
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Three rings, each having radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is:
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
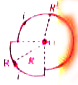
View SolutionTwo rings of same mass and radius R are placed with their planes perpendicular to each other and centre at a common point. The radius of gyration of the system about an axis passing through the centre and perpendicular to the plane of one ring is
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
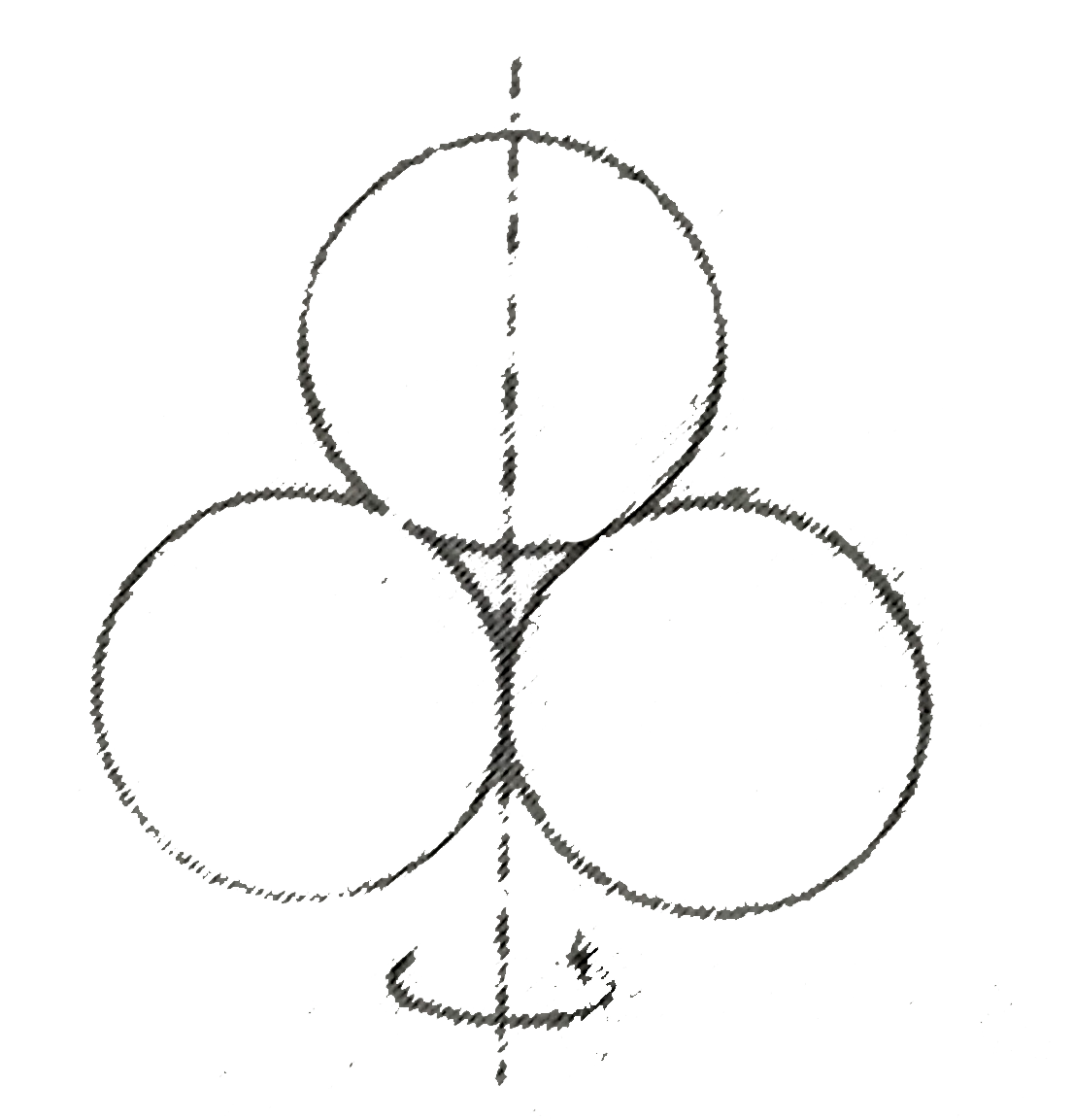
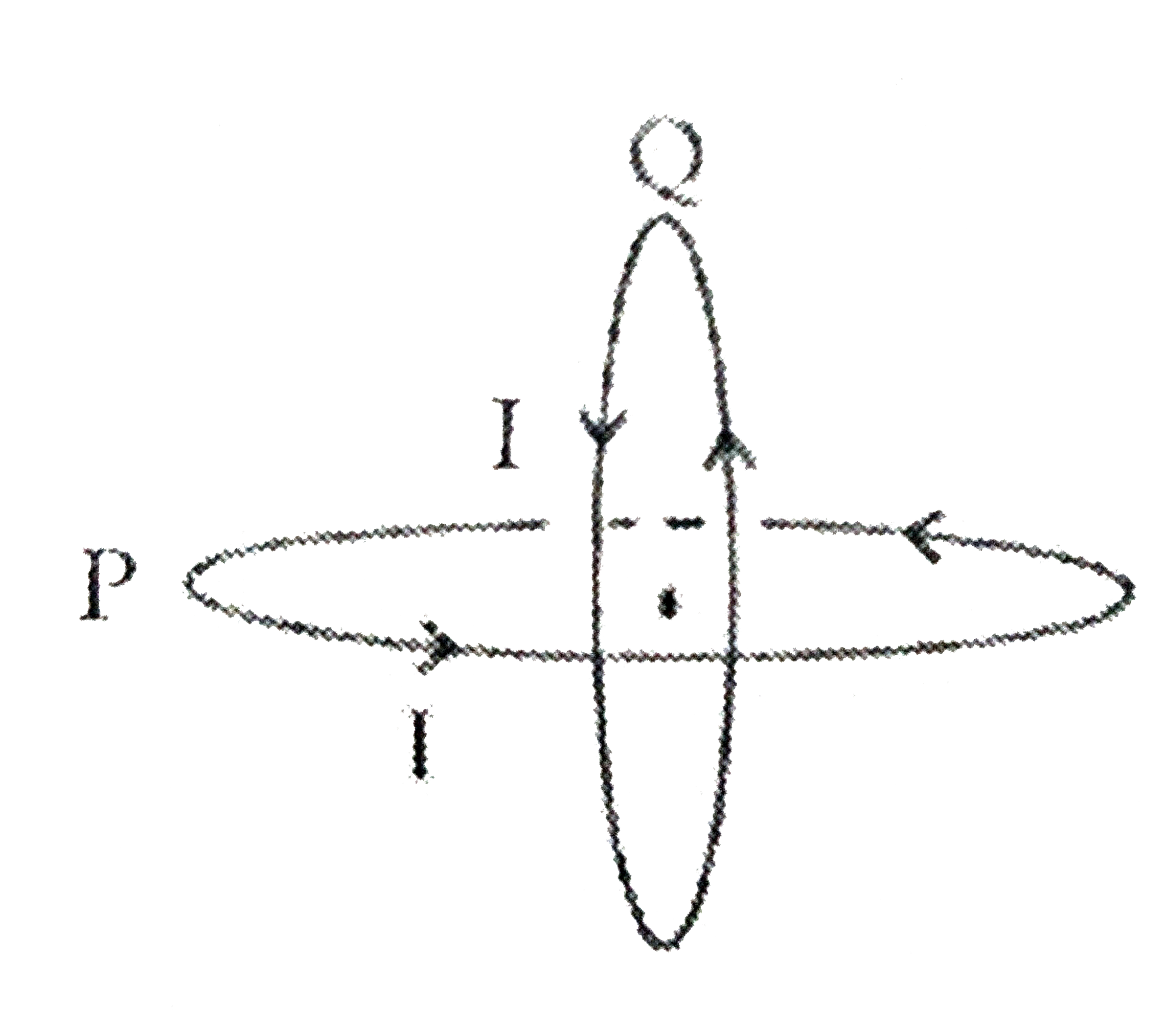
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionThere are two concentric circular loops. One loop of radius r is made up of only one turn. The other loop has a radius 2r and has two turns of wire. They are arranged such that they have a common centre and their planes are perpendicular to each other. When the same current i is passed through both the coils, the magnetic field at the common centre is
View SolutionTwo identical rings each of mass m with their planes mutually perpendicular, radius R are welded at their point of contact O. If the system is free to rotate about an axis passing through the point P perpendicular to the plane of the paper, then the moment of in inertia of the system about this axis is equal to

View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
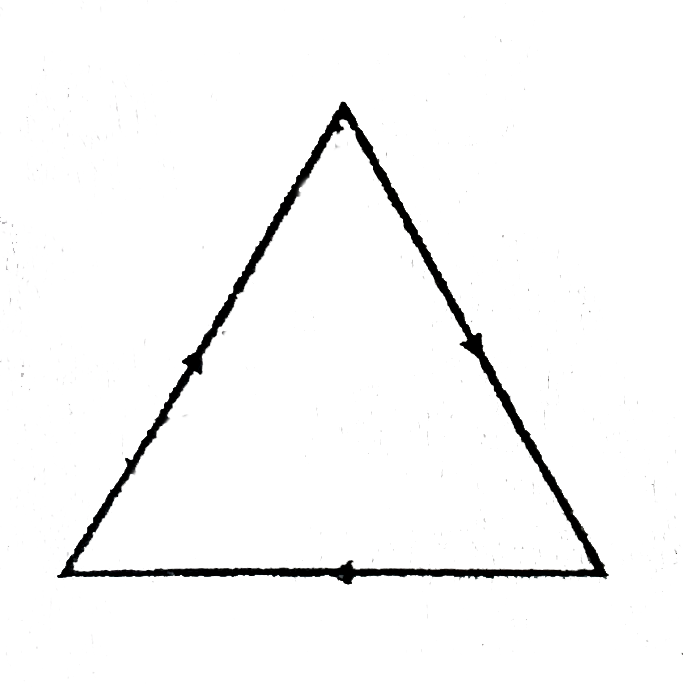
View SolutionTwo circular rings each of radius a are joined together such that their planes are perpendicular to each other as shown in the figure. The resistance of each half part of the ring is indicated. A very small loop of mass m and radius r carrying a current I0 is placed in the plane of the paper at the common centre of each ring. The loop can freely rotate about any of its diametric axes. If the loop is slightly dispalced, find the time period of its oscillations.
(Given ma=2πμ0I0π2

View Solution
