Three rings, each having radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is:
√3μ0I2R
Zero
(√2−1)μ0I2R
(√3−√2)μ0I2R
The correct Answer is:A
To find the magnitude of the magnetic field at the common center of three mutually perpendicular rings, each carrying a current I, we can follow these steps:
Step 1: Understand the Configuration
We have three rings, each with radius R, placed mutually perpendicular to each other. The centers of all three rings are at the origin of the coordinate system.
Step 2: Magnetic Field Due to a Single Ring
The magnetic field B at the center of a single ring carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
Step 3: Determine the Direction of Magnetic Fields
- For the first ring (let's say it lies in the XY-plane), the magnetic field at the center will be directed along the Z-axis.
- For the second ring (in the YZ-plane), the magnetic field will be directed along the X-axis.
- For the third ring (in the XZ-plane), the magnetic field will be directed along the Y-axis.
Step 4: Write the Magnetic Fields
Let’s denote the magnetic fields due to the three rings as B1, B2, and B3:
- B1=μ0I2R^k (along Z)
- B2=μ0I2R^i (along X)
- B3=μ0I2R^j (along Y)
Step 5: Calculate the Magnitude of the Resultant Magnetic Field
The total magnetic field B at the center is the vector sum of the individual magnetic fields:
B=B1+B2+B3
Since these fields are mutually perpendicular, we can use the Pythagorean theorem to find the magnitude:
|B|=√B21+B22+B23
Substituting the values:
|B|=√(μ0I2R)2+(μ0I2R)2+(μ0I2R)2
|B|=√3(μ0I2R)2
|B|=μ0I2R√3
Step 6: Final Result
Thus, the magnitude of the magnetic field at the common center is:
|B|=μ0I√32R
We have three rings, each with radius R, placed mutually perpendicular to each other. The centers of all three rings are at the origin of the coordinate system.
The magnetic field B at the center of a single ring carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
- For the first ring (let's say it lies in the XY-plane), the magnetic field at the center will be directed along the Z-axis.
- For the second ring (in the YZ-plane), the magnetic field will be directed along the X-axis.
- For the third ring (in the XZ-plane), the magnetic field will be directed along the Y-axis.
Let’s denote the magnetic fields due to the three rings as B1, B2, and B3:
- B1=μ0I2R^k (along Z)
- B2=μ0I2R^i (along X)
- B3=μ0I2R^j (along Y)
The total magnetic field B at the center is the vector sum of the individual magnetic fields:
B=B1+B2+B3
Since these fields are mutually perpendicular, we can use the Pythagorean theorem to find the magnitude:
|B|=√B21+B22+B23
Substituting the values:
|B|=√(μ0I2R)2+(μ0I2R)2+(μ0I2R)2
|B|=√3(μ0I2R)2
|B|=μ0I2R√3
Thus, the magnitude of the magnetic field at the common center is:
|B|=μ0I√32R
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Main (Archive)
Explore 75 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 1
Explore 75 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
Similar Questions
Three rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is

View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is

View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is

View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
View SolutionTwo rings of same mass and radius R are placed with their planes perpendicular to each other and centre at a common point. The radius of gyration of the system about an axis passing through the centre and perpendicular to the plane of one ring is
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
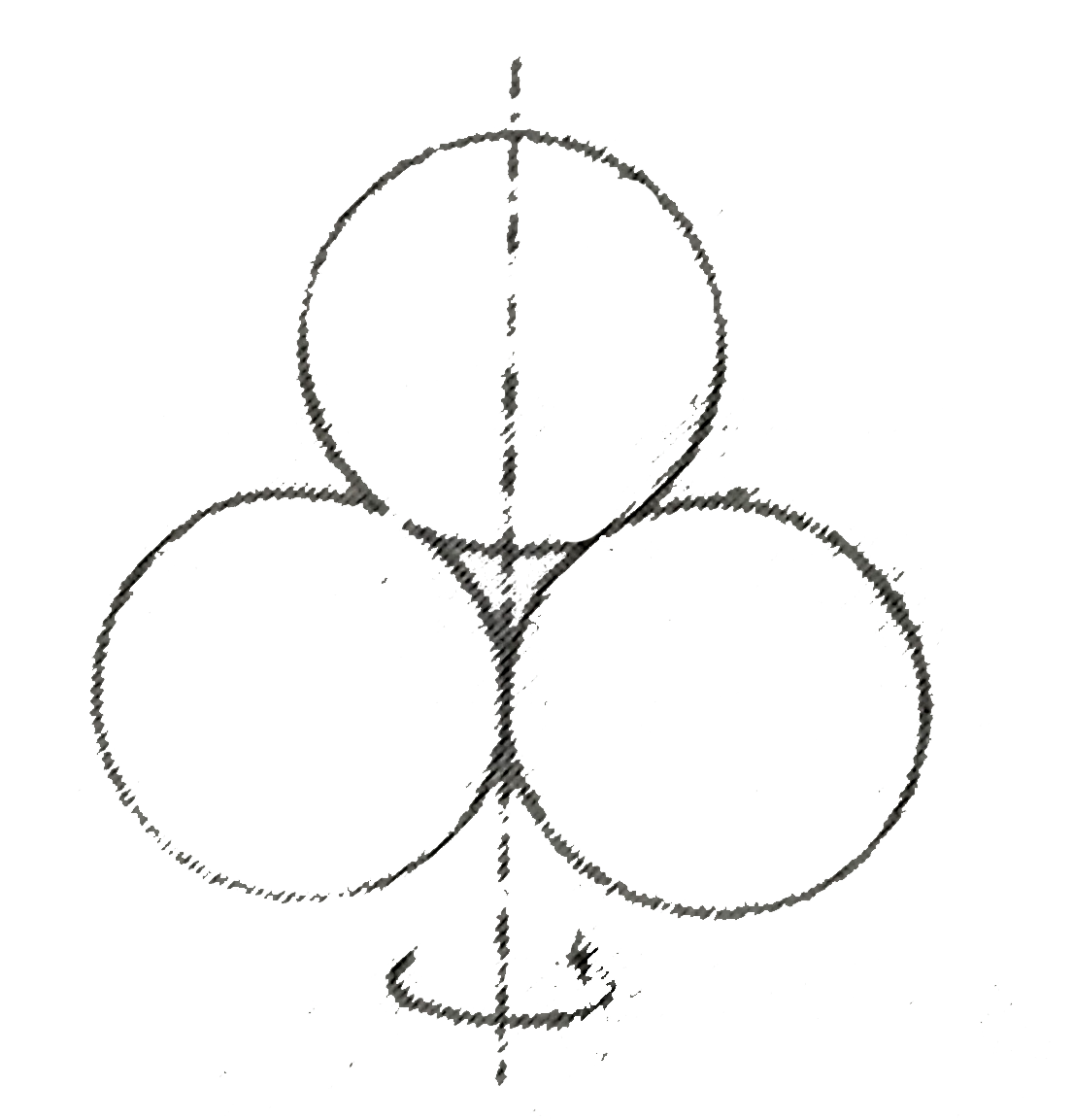
View SolutionThere are two concentric circular loops. One loop of radius r is made up of only one turn. The other loop has a radius 2r and has two turns of wire. They are arranged such that they have a common centre and their planes are perpendicular to each other. When the same current i is passed through both the coils, the magnetic field at the common centre is
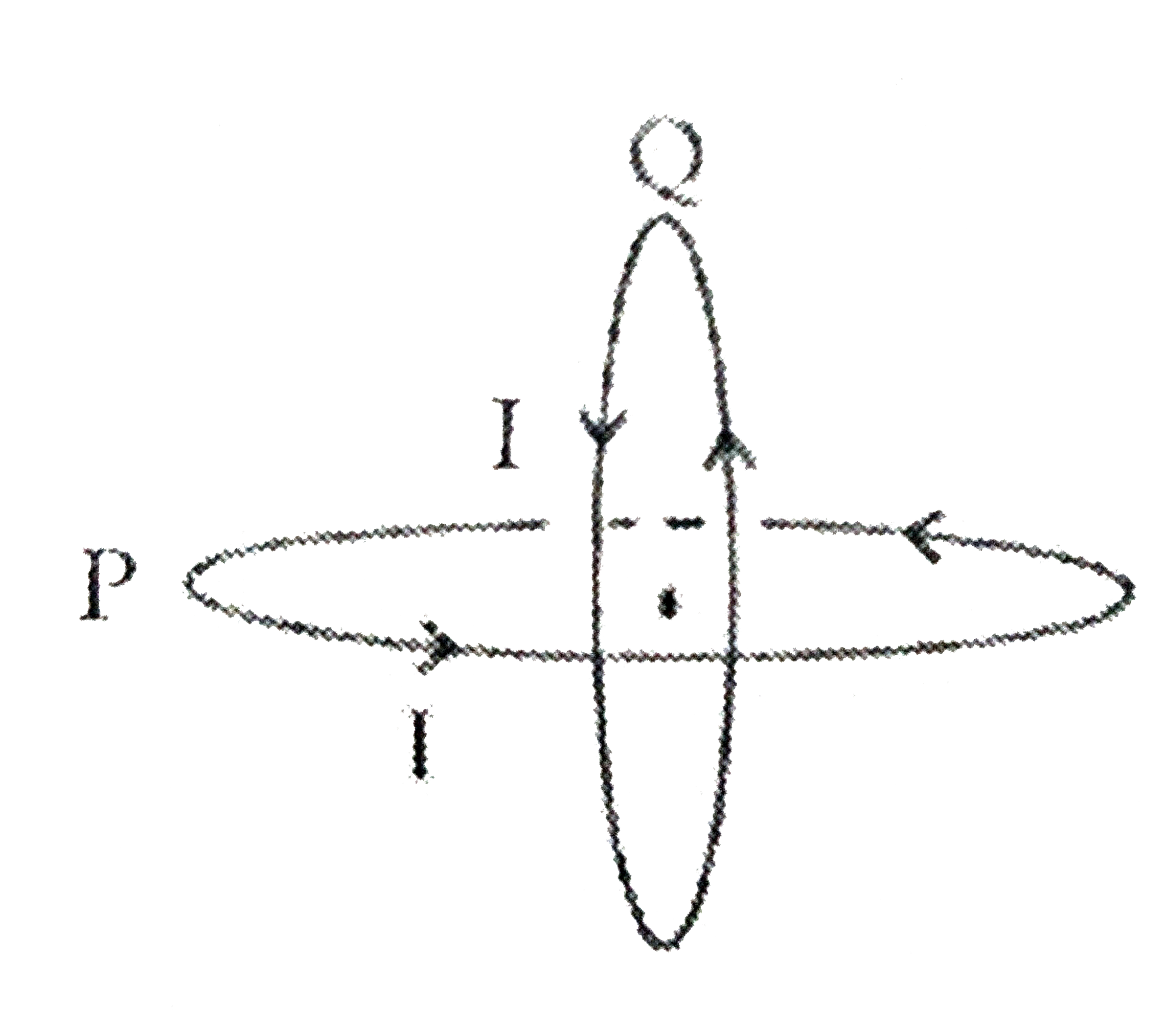
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo identical rings each of mass m with their planes mutually perpendicular, radius R are welded at their point of contact O. If the system is free to rotate about an axis passing through the point P perpendicular to the plane of the paper, then the moment of in inertia of the system about this axis is equal to

View Solution