Two circular rings each of radius a are joined together such that their planes are perpendicular to each other as shown in the figure. The resistance of each half part of the ring is indicated. A very small loop of mass m and radius r carrying a current I0 is placed in the plane of the paper at the common centre of each ring. The loop can freely rotate about any of its diametric axes. If the loop is slightly dispalced, find the time period of its oscillations.
(Given ma=2πμ0I0π2

The equivalent resistance of the circuit is
1Req=3+12
⇒Req=27Ω
∴I=total current =EReq=7amp.
The magnetic field at the centre of the loop is
B=μ0(2)4a+μ0(2)4a−μ0(2)4a−μ0(I)4a
⇒B=μ04a (inward)
The magnetic moments of the tiny ring is M=I0A=πI0r2
If the ring is rotated through angle θ, then restoring torque is
τ=−MBsinθ=−πI0r2μ04aθ (for small angle)
Using IInd law of motion
τ=mr22d2θdt2=−πI0r2μ04aθ
∴T=2π√2maπμ0I0
Similar Questions
A circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
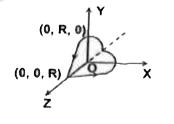
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
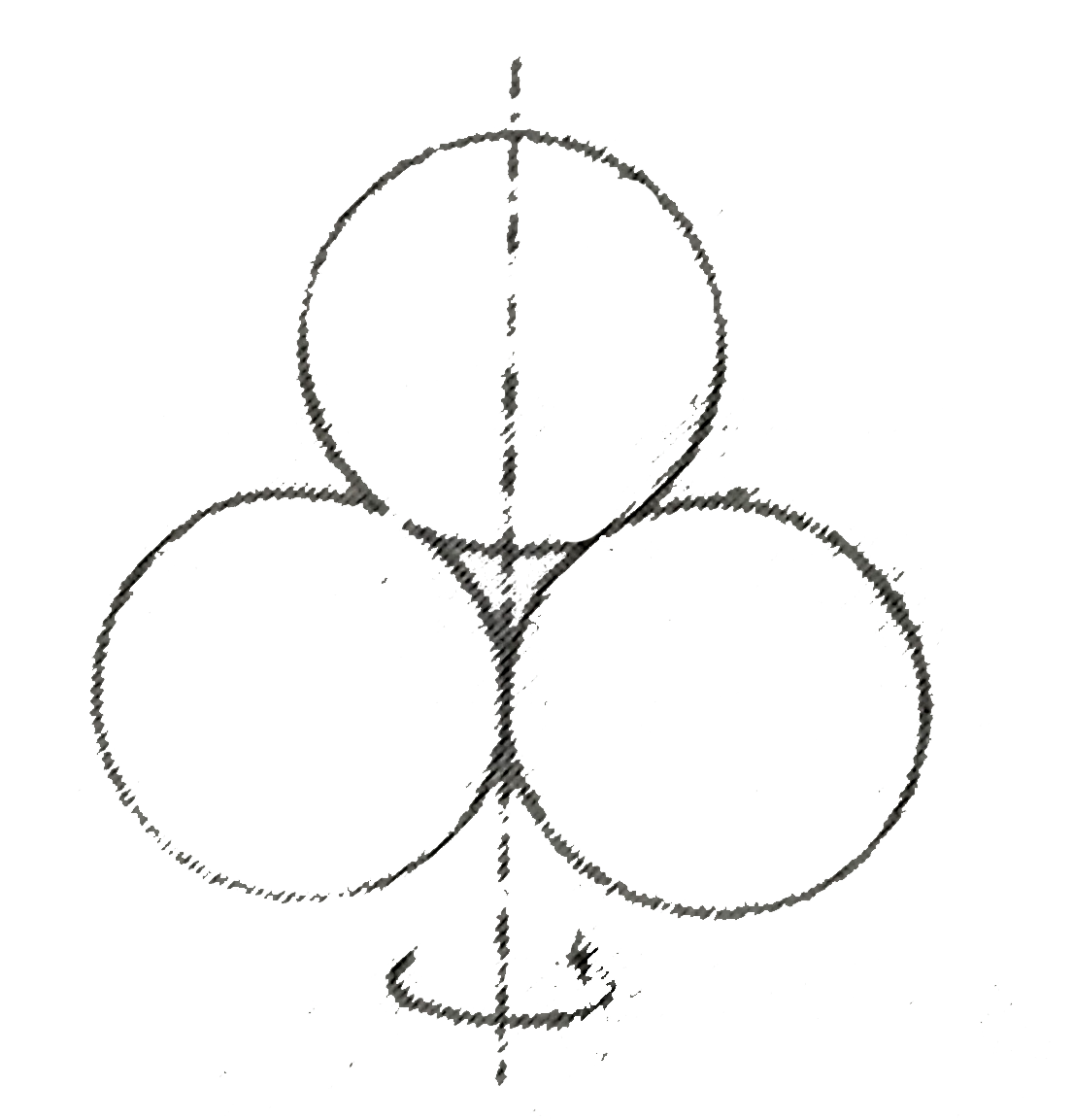
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
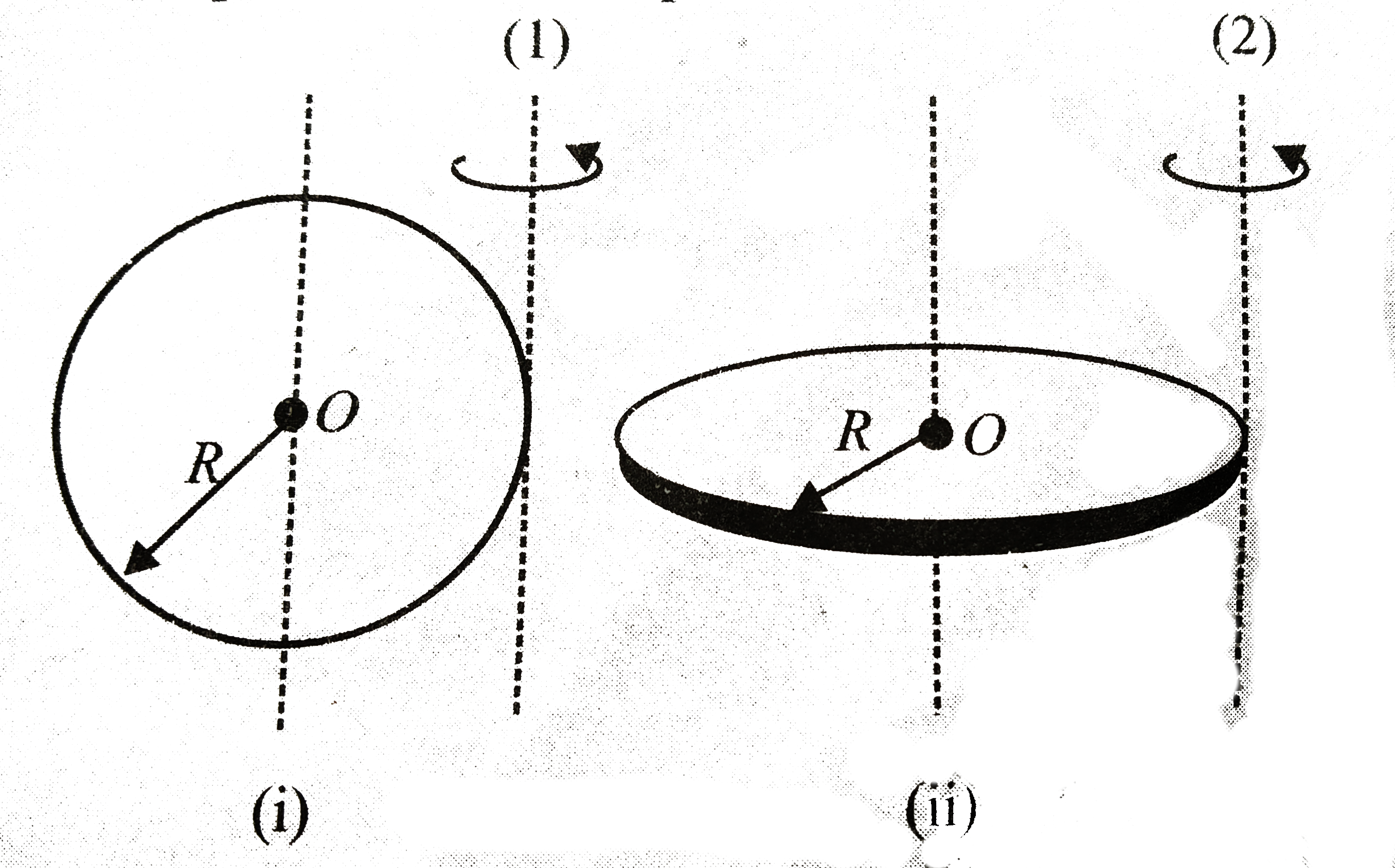
View SolutionTwo loops carrying current in opposite sence placed paralled to each other are moved closer to each other. Then the current

View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionTwo similar circular loops of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and I√3 respectively. The magnetic field at the centre of the coil is
View SolutionTwo rings of same mass and radius R are placed with their planes perpendicular to each other and centre at a common point. The radius of gyration of the system about an axis passing through the centre and perpendicular to the plane of one ring is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
