A rod of weight $w$ is supported by two parallel knife edges $A$ and $B$ and is in equilibrium in a horizontal position. The knives are at a distance $d$ from each other. The centre of mass of the rod is at a distance $x$ from $A$ .

A

$\frac{W d}{x}$

B

$\frac{W (d - x)}{x}$

C

$\frac{W (d - x)}{d}$

D

$\frac{W x}{d}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$N_{A} + N_{B} = m g = W$
$N_{A} x = N_{B} (d - x)$
$\Rightarrow N_{A} x = (m g - N_{A}) (d - x)$
$\Rightarrow N_{A} x = W (d - x) - N_{A} (d - x)$
$\Rightarrow N_{A} d = W (d - x) \Rightarrow N_{A} = \frac{W (d - x)}{d}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

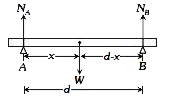
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position . The knives are at a distance d from each other . The centre of mass of the rod is at distance x from A . The normal reaction on A is
A $\frac{W (d - x)}{x}$
B $\frac{W (d - x)}{d}$
C $\frac{W x}{d}$
D $\frac{W d}{x}$
Question 2 - Select One
A uniform metre rod is bent into $L$ shape with the bent arms at $90^{\circ}$ to each other. The distance of the centre of mass from the bent point is
A $\frac{L}{4 \sqrt{2}} m$
B $\frac{L}{2 \sqrt{2}} m$
C $\frac{L}{\sqrt{2}} m$
D $\frac{L}{8 \sqrt{2}} m$
Question 3 - Select One
A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed $ω$ in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

A $\frac{49 m L^{2} ω^{2}}{24}$
B $2 m ω^{2} L^{2}$
C $\frac{1}{24} m ω^{2} L^{2}$
D $\frac{13 m L^{2} ω^{2}}{24}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)

Home
Ask Doubt
Profile