Consider two masses with m1>m2 connected by a light inextensible string that passes over a pulley of radius R and moment of inertia I about its axis of rotation. The string does not slip on the pulley and the pulley turns without friction. The two masses are released from rest separated by a vertical distance 2h. When the two masses pass each other, the speed of the masses is proportional to
⎷m1−m2m1+m2+IR2
⎷(m1+m2)(m1−m2)m1+m2+IR2
⎷m1+m2+IR2m1−m2
⎷IR2m1+m2
The correct Answer is:A
m1g−T2=m1a ..(i)
T2−m2g=m2a ....(ii)
(T1−T2)R=IRa ....(iii)
a=(m1−m2)g(IR2+m1+m2)⇒v2rel=8hg(m1−m2)(IR2+m1+m2)
As vrel=v−(−v)=2v⇒v=12
⎷8gh(m1−m2)(IR2+m1+m2)
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)
44 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
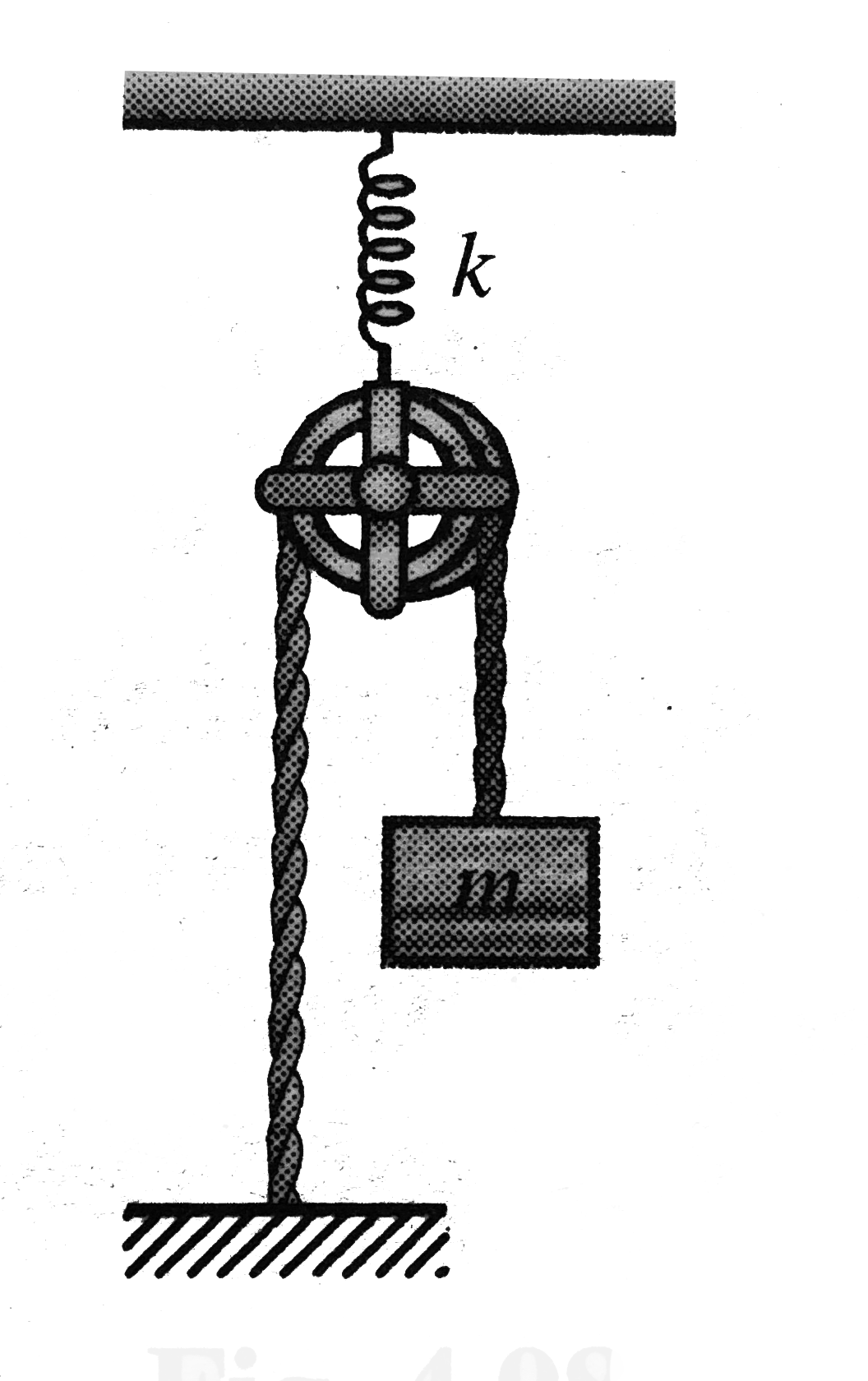
View Solution
Knowledge Check
Consider two object with m1>m2 connected by a light string that passes over a pulley having a moment of inertia of I about its axis of rotation as shown in figure. The string does not slip on the pulley or strech. The pulley turns without friction. The two objects are released from rest separated by a vertical distance 2h. The translational speeds of the objects as they pass each other is.
 .A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2
.A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
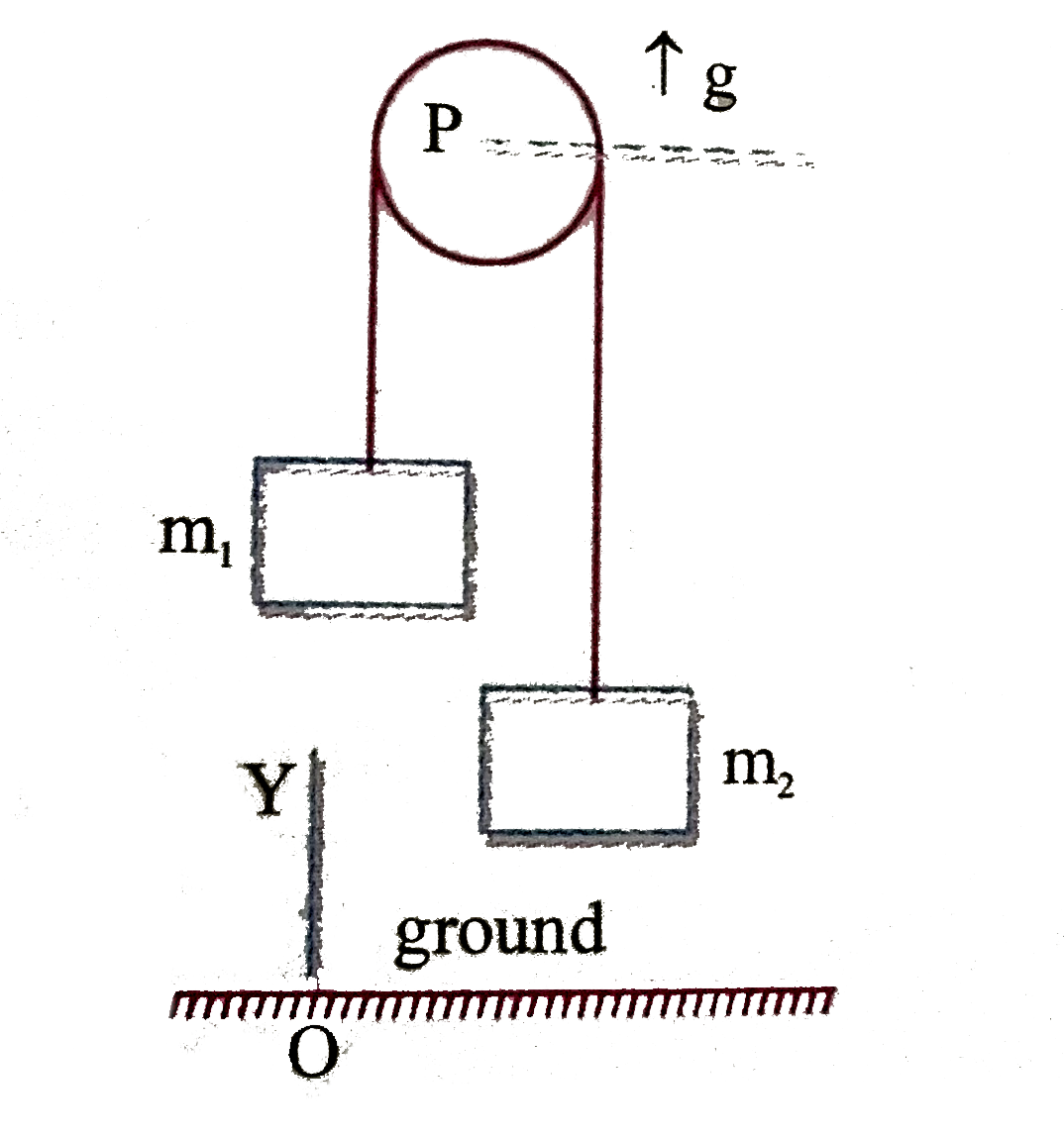 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2gTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
Consider the situation as shown in the figure. If m1>m2, I is the moment of intertia about its axis of rotation, R is the radius of pulley. The objects are released from rest separated by a vertical distance 2h. Find the translational speed of the objects as they pass each other. Assume no slipping.
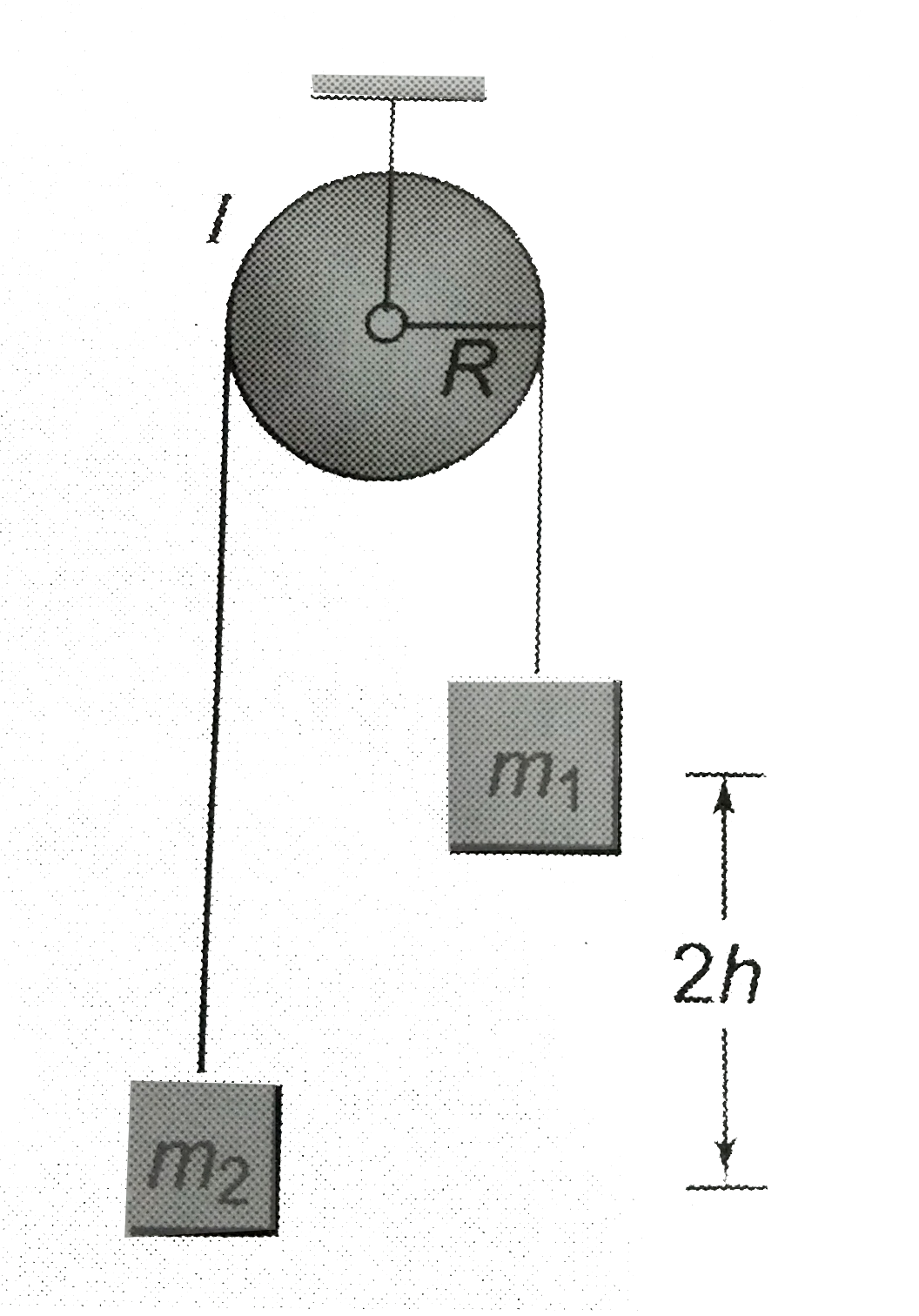
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley Fibd the acceleration of the masses and tension in the string , when the masses are released
 .
.
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionAn object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionTwo particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
View Solution
