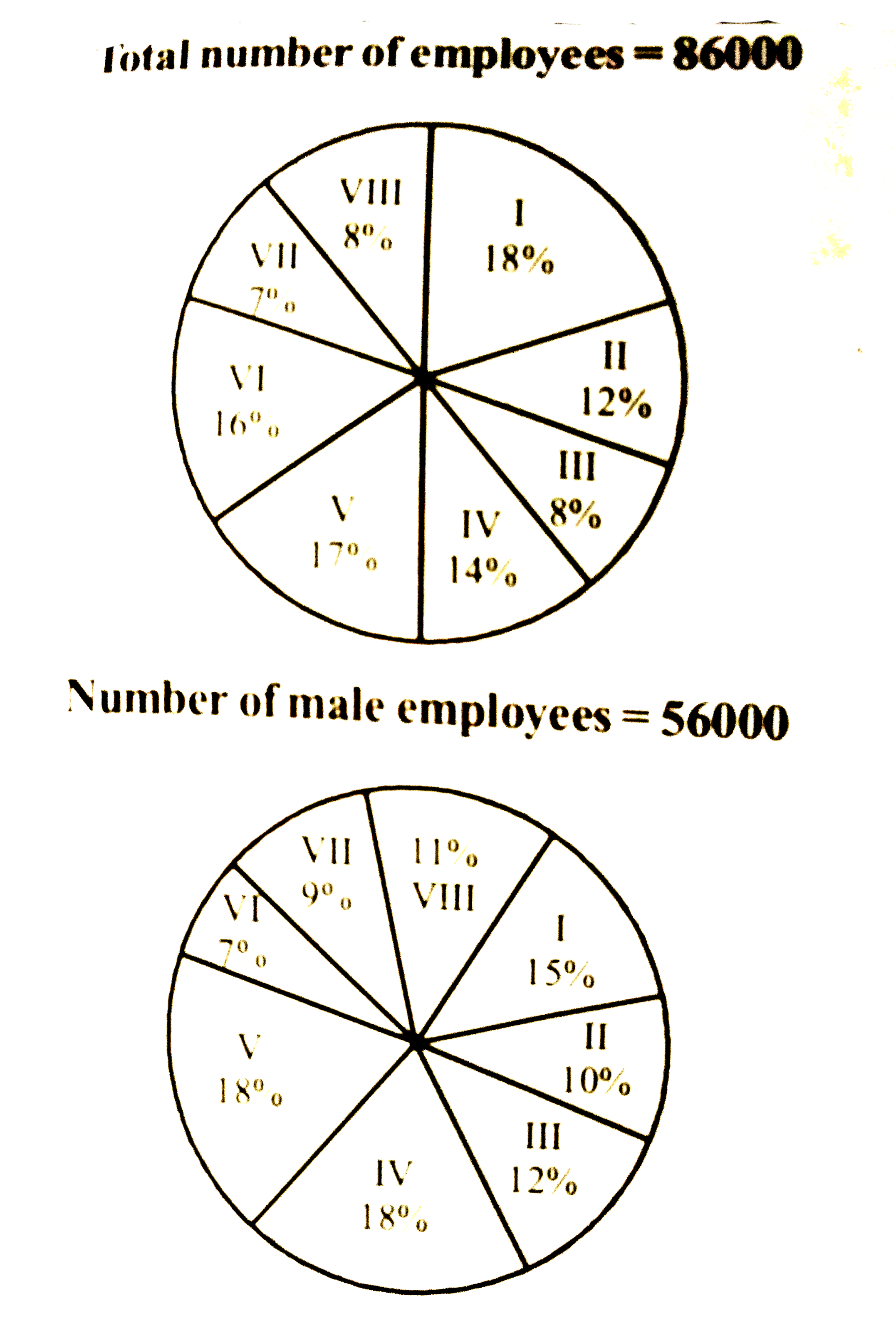Given data shows total male and female employee in three companies in a seminar. Read data carefully and answer the questions:
In annual seminar of three companies, A, B and C some male and female employees represent their companies. Average number of female employees who represent A and B is 420. Total male employee in A and B is 1620. Number of female employees is 23 rd and 25 th of male employee in A and B respectively. Total female employee who represent C are 25% more than total female employee who represent A and total male employee who represent C are 33 13% more than total female employee who represent B.
Find average number female in B & C?
480
420
520
540
The correct Answer is:A
To solve the problem step by step, we will analyze the information provided and calculate the required values.
Step 1: Calculate Total Female Employees in A and B
The average number of female employees who represent companies A and B is given as 420. Therefore, the total number of female employees in A and B can be calculated as:
Total female employees in A and B=420×2=840
Hint: To find the total from an average, multiply the average by the number of entities (in this case, companies).
Step 2: Set Up Equations for Male and Female Employees
Let the number of male employees in company A be X. Then, the number of male employees in company B will be 1620−X (since the total male employees in A and B is 1620).
According to the problem:
- The number of female employees in A is 23X.
- The number of female employees in B is 25(1620−X).
Step 3: Create an Equation for Female Employees
The total number of female employees in A and B can be expressed as:
23X+25(1620−X)=840
Hint: Combine the expressions for female employees from both companies to form an equation.
Step 4: Solve the Equation
To solve the equation, we first find a common denominator (which is 15):
10X15+2(1620−X)15=840
This simplifies to:
10X+3240−2X=12600(Multiplying through by 15)
Combining like terms gives:
8X+3240=12600
Subtracting 3240 from both sides:
8X=9360
Dividing by 8:
X=1170
Hint: Isolate the variable by performing inverse operations.
Step 5: Calculate Male and Female Employees in A and B
Now that we have X:
- Male employees in A = 1170
- Male employees in B = 1620−1170=450
Now, calculate the female employees:
- Female employees in A = 23×1170=780
- Female employees in B = 25×450=180
Step 6: Calculate Total Female Employees in C
The total female employees in C are 25% more than those in A:
Female employees in C=780+0.25×780=780×1.25=975
Hint: To find a percentage increase, multiply the original number by (1 + percentage increase).
Step 7: Calculate Total Male Employees in C
The total male employees in C are 33.33% more than those in B:
Male employees in C=450+13×450=450×43=600
Step 8: Calculate Average Number of Female Employees in B and C
Finally, we find the average number of female employees in B and C:
Average=Female in B+Female in C2=180+9752=11552=577.5
Hint: To find the average, sum the values and divide by the number of values.
Conclusion
The average number of female employees in B and C is 577.5.
The average number of female employees who represent companies A and B is given as 420. Therefore, the total number of female employees in A and B can be calculated as:
Total female employees in A and B=420×2=840
Let the number of male employees in company A be X. Then, the number of male employees in company B will be 1620−X (since the total male employees in A and B is 1620).
- The number of female employees in A is 23X.
- The number of female employees in B is 25(1620−X).
The total number of female employees in A and B can be expressed as:
23X+25(1620−X)=840
To solve the equation, we first find a common denominator (which is 15):
10X15+2(1620−X)15=840
This simplifies to:
10X+3240−2X=12600(Multiplying through by 15)
Combining like terms gives:
8X+3240=12600
Subtracting 3240 from both sides:
8X=9360
Dividing by 8:
X=1170
Now that we have X:
- Male employees in A = 1170
- Male employees in B = 1620−1170=450
- Female employees in A = 23×1170=780
- Female employees in B = 25×450=180
The total female employees in C are 25% more than those in A:
Female employees in C=780+0.25×780=780×1.25=975
The total male employees in C are 33.33% more than those in B:
Male employees in C=450+13×450=450×43=600
Finally, we find the average number of female employees in B and C:
Average=Female in B+Female in C2=180+9752=11552=577.5
The average number of female employees in B and C is 577.5.
Topper's Solved these Questions
Similar Questions
Knowledge Check
DELL Compouter has two branches : One in Ohilo and second in Texas : The total no. of Ohio office grew this year by 25% to 750 but the ratio of male to female employees is same as in the previous year. The no. of employees in the Texas office grew this year by 9.09% to 1200. The ratio of male to female employees last year in the Texas was 5:6 and the no. of male employees in the Ohio office was 20% less than that of Texas office.
The total no. of employees in both the offices last year was :A1500B1700C1650Dcan't be determinedStudy the given graph and answer the question that follows.
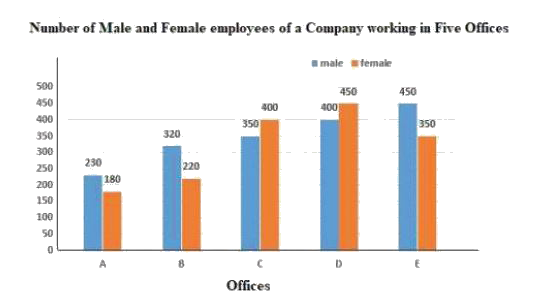
In which office of the company is the number of male employees 25% more than the average number of female employees in all five offices?ADBBCEDCThe average salary of male employees in a firm was Rs. 5200 and that of female was Rs. 4200 . The mean salary of all the employees was Rs. 5000 . What is the percentage of female employees ?
A40%B30%C25%D20%
Study the following table and answer questions: Number of employees working in five different companies.

What percent of total male employees in companies A and B is the number of female employees in E?
View Solution12% of the employees in a factory are females and the number of male employees is 264. Find the total number of employees. Also, find the number of female employees.
View SolutionThe ratio of male and female employees in a multinational company is 5:3. If there are 115 male employees in the company, then the number of female employees is 96 (b) 52 (c) 69 (d) 66
View SolutionDELL Computer has two branches : One in Ohilo and second in Texas : The total no. of Ohio office grew this year by 25% to 750 but the ratio of male to female employees is same as in the previous year. The no. of employees in the Texas office grew this year by 9.09% to 1200. The ratio of male to female employees last year in the Texas was 5:6 and the no. of male employees in the Ohio office was 20% less than that of Texas office.
The total no. female employees this year in both the offices is :
View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different officies (A B C D E ) Total no. of employees=2400
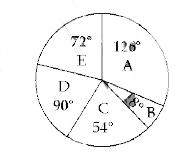
IF the percentage of male employees in office C is 20% and that of female employees in E is 40%, then what is the ratio of the number of female employees in C to that of female employees in E?
View Solution