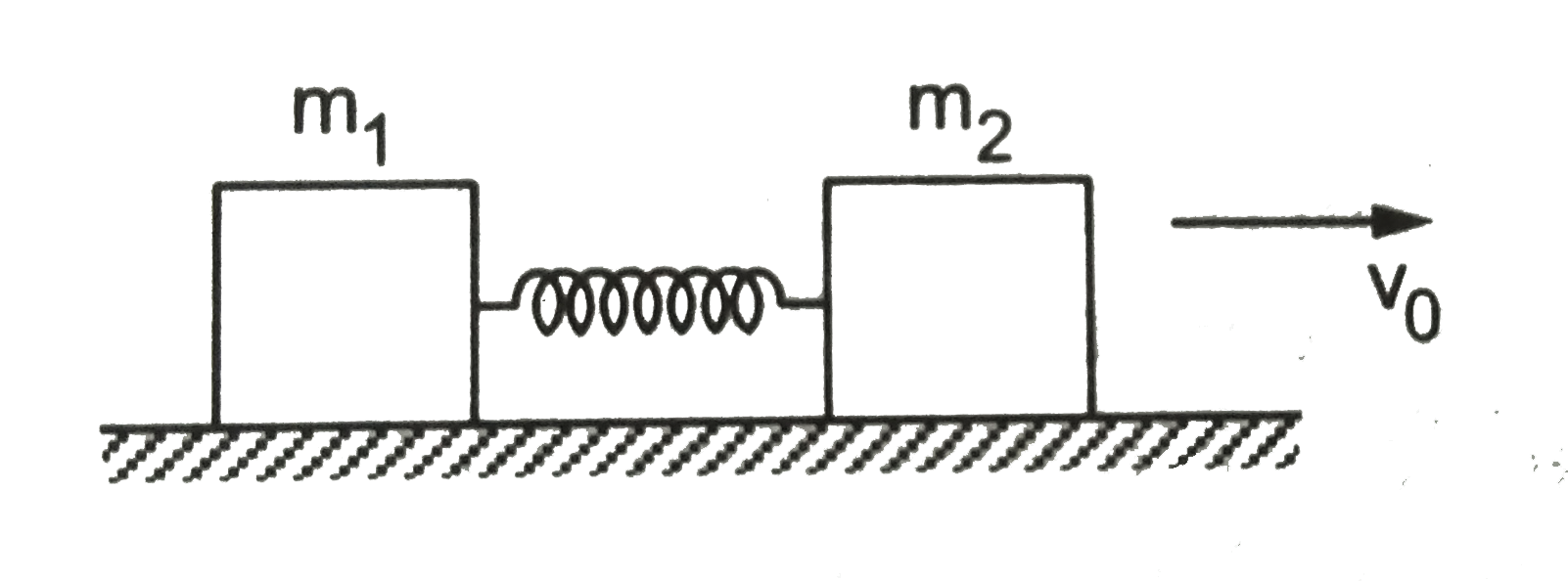
Two blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shapr imulse so that it acquires a velocity v0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.
 Solution in Gujrati
Solution in Gujrati
Velocity of centre of mass
=m1v1+m2v2m1+m2
Hence v1=0,v2=v0
=m1×0+m2×v0m1+m−2
=m2v0m1+m2
b. The spring wil attain maximum elongation when both velocities of two blocks wil attain are veolicy of centre of mass.
x→maxiμmelongationofspr∈g<br>chan≥∈k∈etice≠rgy<br>=potentiale≠rgys→red∈spr∈g<br>rarr 1/2 m_2v_2^2-1/2(m_1+m_2)((m_2v_0)/(m_1+m_2))^2<br>=1/2kx^2<br>rarr m_2v_0^2(1-m^2/(m_1+m_2)=kx^2<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_104_S01.pngwh=80%mx-autosty≤=background:white;><br>rarr x=[(m_1m_2)/(m_1+m_2)]^91/2)V_0
Similar Questions
A spring connects two particles of masses m1andm2 A horizontal force F acts on m1 Ignoring friction, when the elongation of the spring is x then:

View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.

View SolutionTwo blocks of masses m_1 =1kg and m_2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m_(1) is imparted an initial velocity v_(0) = 12cm/s to the right. The amplitude of oscillation is
View SolutionA spring-mass system ( m_1 + massless spring + m_2 ) fall freely from a height h before m_2 colliding inelastically with the ground. Find the maximum value of h so that block m_2 will break off the surface. Assume k=stiffness of the spring.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionTwo identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V_0 maximum extension of spring is
View SolutionThe block of mass m_1 shown in figure is fastened to the spring and the block of mass m_2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2/k)(m_1+m_2)gsintheta against the spring and released. Find the position where the two blocks separate.
View SolutionThe figure shows two blocks of mass m each, which are connected by an ideal elastic spring and then placed on a frictionless floor. As shown, if the blocks are v_0 And 2v_0 The velocity is given, then the maximum extension in the spring is:
View Solution
