A block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.

Position(1): K1=12mv20,Ug1=0,Us1=0
(2): K2=0,Ug2=0,Us1=12kx20
(3): K3=12mv2,Ug3=0,Us3=12k(x02)2
Ug: gravitational potential energy
US: energy stored in spring
By the mechanical energy conservation, we have
K1+Ug1+Us1=K3+Ug2+Us2
12mv20=12kx20⇒x0=v0√mk
x0: maximum compression of spring
K1+Ug1+Us1=K3+Ug3+Us3
12mv20=12mv2+12k(x02)2
=12mv2+12kv204×mK
12mv2=38mv20
⇒v=√32v0
Topper's Solved these Questions
Similar Questions
Knowledge Check
A solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
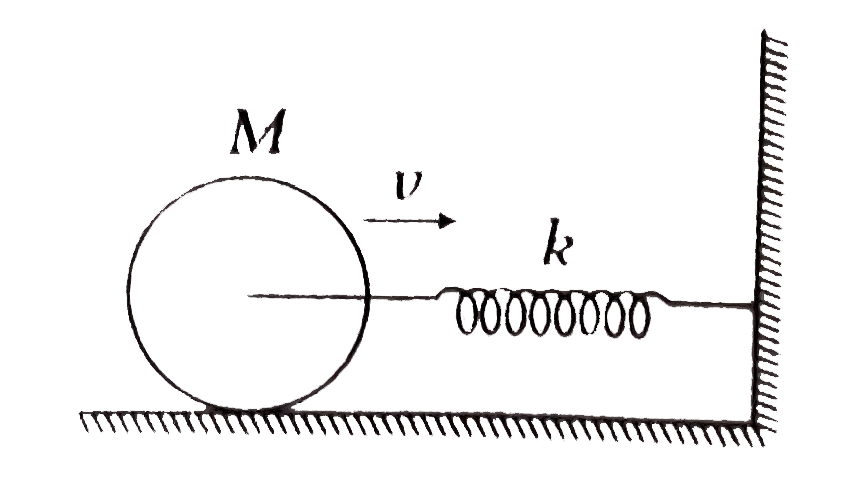 Av√2M3kBv√2M5kCv√5k7MDv√7M5k
Av√2M3kBv√2M5kCv√5k7MDv√7M5kA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View Solution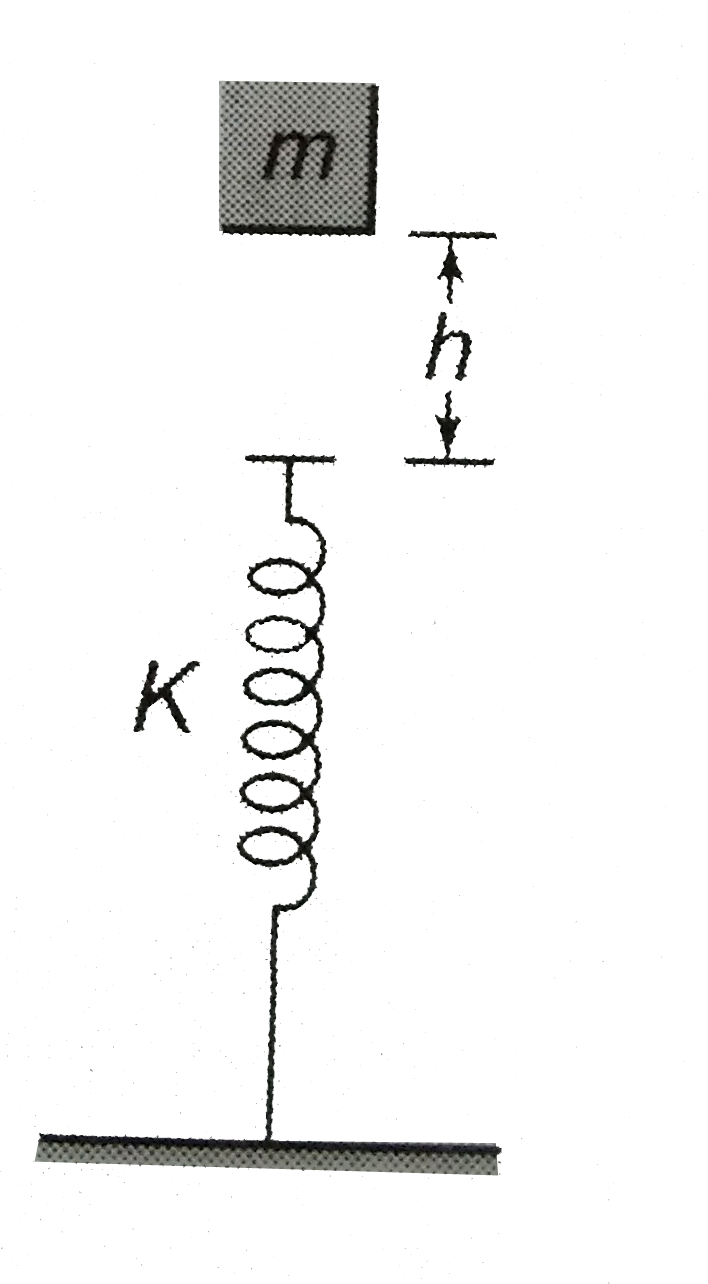
A block is released from height h, find the maximum compression of spring of spring constant k.
View Solution