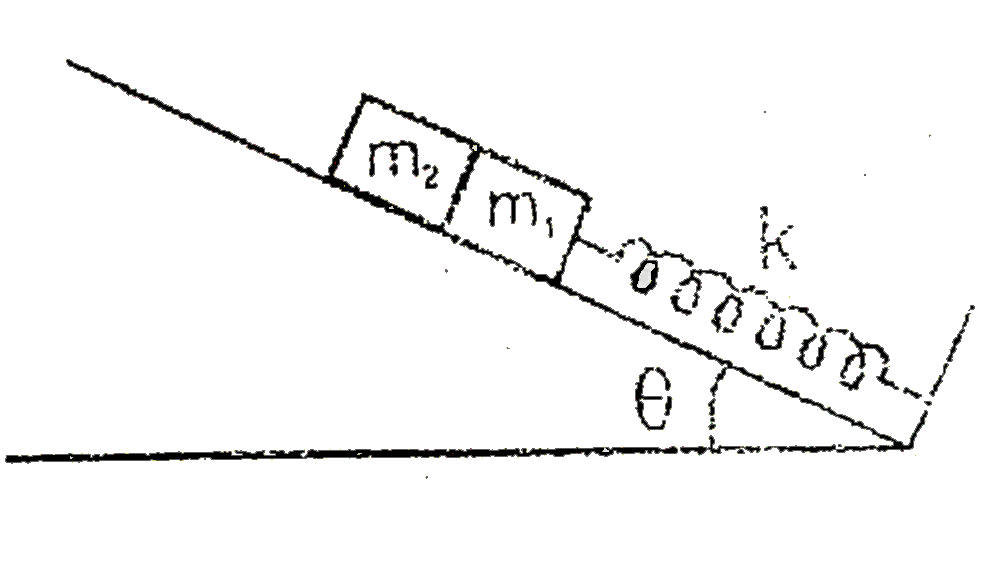
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate.

(√13k(m1+m2))gsinθ
(√2k(m1+m2))gsinθ
(√3k(m1+m2))gsinθ
(√1k(m1+m2))gsinθ
The correct Answer is:C
At equilibrium position : →
Kx0=m1gsinθ+m2gsinθ
x0=(m1+m2)gsinθk
Block will separate when acceleration of block of mass m1 will be just equal to gsinθ
⇒a=ω2x=gsinθ
⇒Km1+m2×x=gsinθ
x=m1+m2Kgsinθ=x0
So, blocks will separate when blocks are at distance x=m1+m2Kgsinθ
From mean position
i.e. spring is at its natural position (amplitude A=(2K(m1+m2)gsinθ'))
Blocks will seoparte at distance x=x0 from mean position.
v=√A2−x20
=√Km1+m2√(2K(m1+m2)gsinθ)2−((m1+m2K)gsinθ)2
=√3k(m1+m2)gsinθ
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - I
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
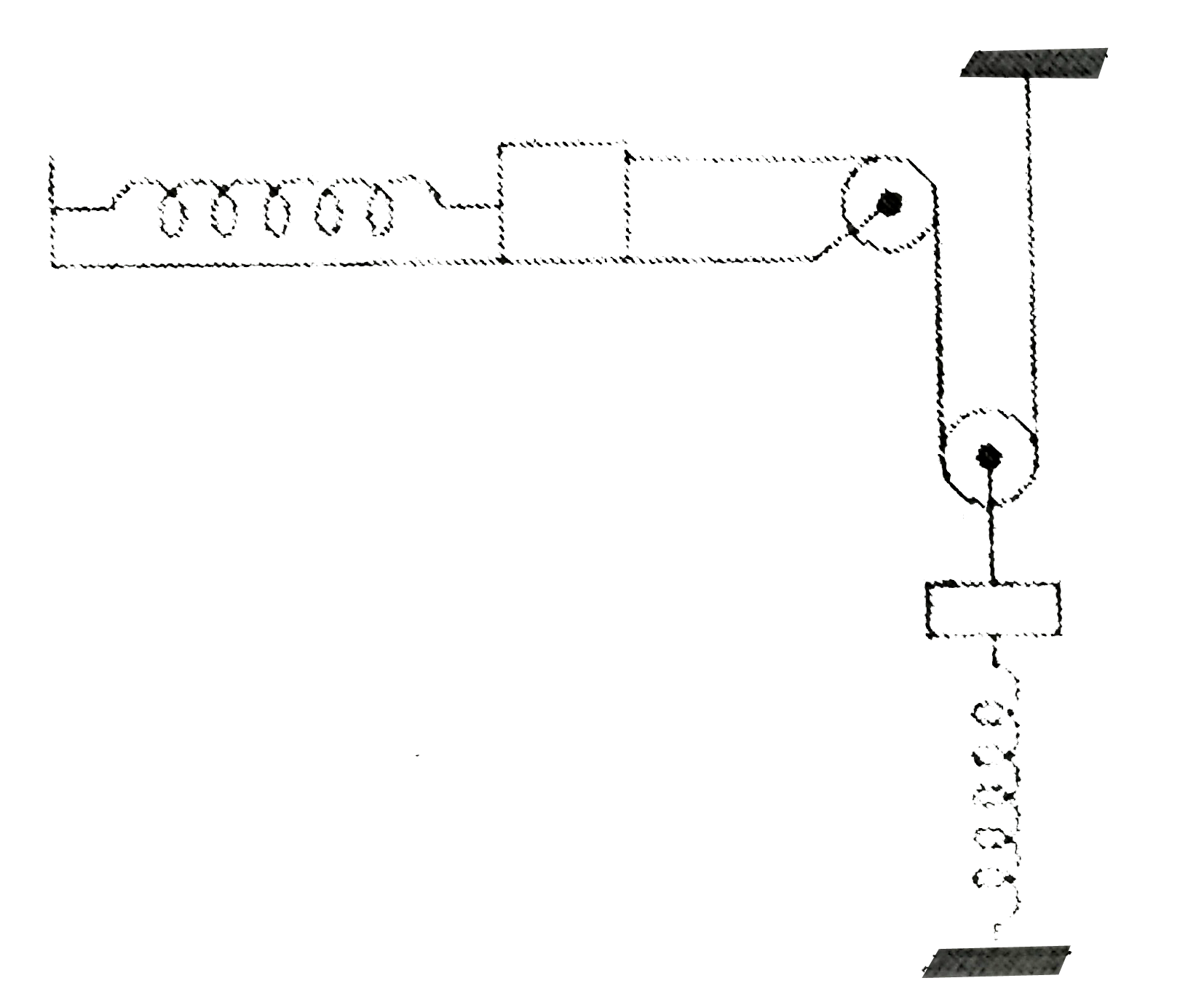
In the equilibrium position, speed of the block placed horizontally is
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View Solution

