A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B. particle released from rest from mid point of AB.
Find the minimum distance of the particle from B during the motion.
A.a6
B.a4
C.a3
D.a8
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the particle and derive the equations of motion.
Step 1: Understanding the Forces
The particle of mass m is subjected to two forces when it is at a point P on the line AB:
1. A force towards A: \( F_A = \frac{mg \cdot AP}{a} \)
2. A force towards B: \( F_B = \frac{2mg \cdot BP}{a} \)
Where:
- \( AP \) is the distance from point A to point P.
- \( BP \) is the distance from point B to point P.
Step 2: Defining Distances
Let:
- The total length of the line AB be a.
- The distance from A to P be \( AP = \frac{a}{2} - x \) (where x is the distance from B to P).
- The distance from B to P be \( BP = x \).
Step 3: Expressing the Forces
Substituting the distances into the force equations:
- Force towards A:
\(
F_A = \frac{mg \left(\frac{a}{2} - x\right)}{a} = \frac{mg}{a} \left(\frac{a}{2} - x\right)
\)
- Force towards B:
\(
F_B = \frac{2mg \cdot x}{a}
\)
Step 4: Finding the Net Force
The net force \( F_{net} \) acting on the particle is the difference between the forces:
\(
F_{net} = F_B - F_A = \frac{2mg \cdot x}{a} - \frac{mg}{a} \left(\frac{a}{2} - x\right)
\)
Simplifying this:
\(
F_{net} = \frac{mg}{a} \left(2x - \left(\frac{a}{2} - x\right)\right) = \frac{mg}{a} \left(3x - \frac{a}{2}\right)
\)
Step 5: Setting Up the Equation of Motion
Using Newton's second law, \( F = ma \):
\(
ma = \frac{mg}{a} \left(3x - \frac{a}{2}\right)
\)
Dividing both sides by m:
\(
a = \frac{g}{a} \left(3x - \frac{a}{2}\right)
\)
Step 6: Identifying Simple Harmonic Motion
This equation can be rearranged to resemble the standard form of simple harmonic motion:
\(
\frac{d^2x}{dt^2} = -\frac{3g}{a} x + \frac{g}{2a}
\)
This indicates that the particle undergoes simple harmonic motion with an equilibrium position at \( x = \frac{a}{6} \).
Step 7: Finding the Minimum Distance from B
The amplitude of the motion can be calculated as:
\(
\text{Amplitude} = \frac{a}{2} - \frac{a}{6} = \frac{3a}{6} - \frac{a}{6} = \frac{2a}{6} = \frac{a}{3}
\)
Thus, the minimum distance from B during the motion is:
\(
\text{Minimum distance} = \frac{a}{3} - \frac{a}{6} = \frac{2a}{6} = \frac{a}{6}
\)
Final Answer
The minimum distance of the particle from B during the motion is:
\(
\boxed{\frac{a}{6}}
\)
The particle of mass m is subjected to two forces when it is at a point P on the line AB:
1. A force towards A: \( F_A = \frac{mg \cdot AP}{a} \)
2. A force towards B: \( F_B = \frac{2mg \cdot BP}{a} \)
- \( AP \) is the distance from point A to point P.
- \( BP \) is the distance from point B to point P.
Let:
- The total length of the line AB be a.
- The distance from A to P be \( AP = \frac{a}{2} - x \) (where x is the distance from B to P).
- The distance from B to P be \( BP = x \).
Substituting the distances into the force equations:
- Force towards A:
\(
F_A = \frac{mg \left(\frac{a}{2} - x\right)}{a} = \frac{mg}{a} \left(\frac{a}{2} - x\right)
\)
- Force towards B:
\(
F_B = \frac{2mg \cdot x}{a}
\)
The net force \( F_{net} \) acting on the particle is the difference between the forces:
\(
F_{net} = F_B - F_A = \frac{2mg \cdot x}{a} - \frac{mg}{a} \left(\frac{a}{2} - x\right)
\)
Simplifying this:
\(
F_{net} = \frac{mg}{a} \left(2x - \left(\frac{a}{2} - x\right)\right) = \frac{mg}{a} \left(3x - \frac{a}{2}\right)
\)
Using Newton's second law, \( F = ma \):
\(
ma = \frac{mg}{a} \left(3x - \frac{a}{2}\right)
\)
Dividing both sides by m:
\(
a = \frac{g}{a} \left(3x - \frac{a}{2}\right)
\)
This equation can be rearranged to resemble the standard form of simple harmonic motion:
\(
\frac{d^2x}{dt^2} = -\frac{3g}{a} x + \frac{g}{2a}
\)
This indicates that the particle undergoes simple harmonic motion with an equilibrium position at \( x = \frac{a}{6} \).
The amplitude of the motion can be calculated as:
\(
\text{Amplitude} = \frac{a}{2} - \frac{a}{6} = \frac{3a}{6} - \frac{a}{6} = \frac{2a}{6} = \frac{a}{3}
\)
Thus, the minimum distance from B during the motion is:
\(
\text{Minimum distance} = \frac{a}{3} - \frac{a}{6} = \frac{2a}{6} = \frac{a}{6}
\)
The minimum distance of the particle from B during the motion is:
\(
\boxed{\frac{a}{6}}
\)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - I
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find its time period when released from rest from mid-point of line AB.
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.
View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionA particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is

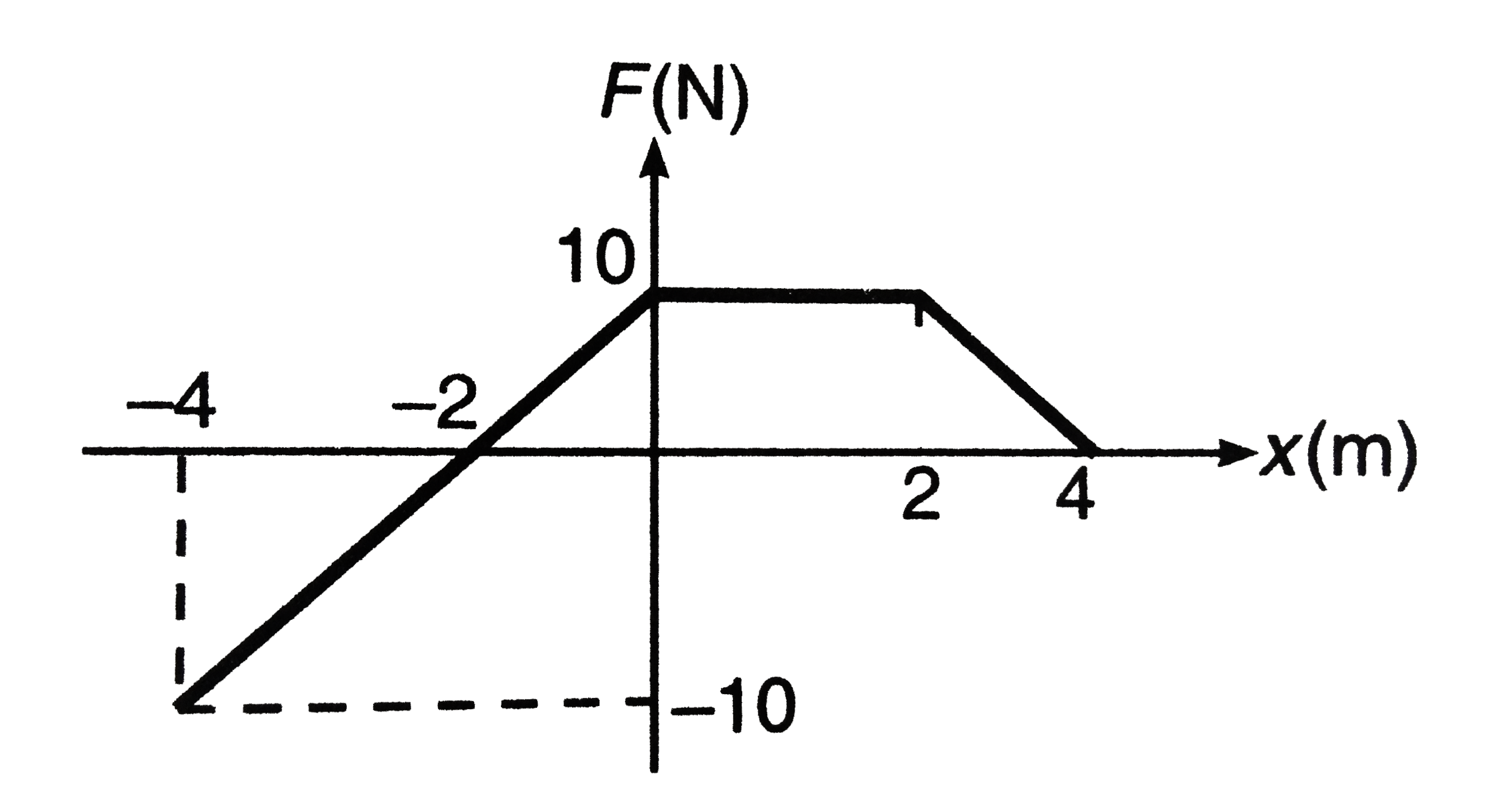
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
 .
.
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
View SolutionA particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by −kx2ˆi. If the particle starts from rest at x=a, the speed it will attain when it crosses the origin is
View Solution

