A particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
To solve the problem of finding the work done by gravity as a particle of mass m is released from point A in a smooth hemispherical bowl and reaches the lowest point B, we can follow these steps:
1. Identify the Initial and Final Positions:
- The particle is released from point A, which is at the top of the hemispherical bowl.
- The lowest point B is at the bottom of the bowl.
2. Determine the Height:
- Let the radius of the hemispherical bowl be r. The height h of the particle at point A is equal to the radius r of the bowl, so h=r.
3. Calculate Initial Potential Energy:
- The potential energy (PE) at point A can be calculated using the formula:
PEA=mgh=mg(r)
- Since h=r, we have:
PEA=mgr
4. Calculate Final Potential Energy:
- At point B (the lowest point), the height is 0, so the potential energy at point B is:
PEB=mg(0)=0
5. Apply the Work-Energy Principle:
- According to the work-energy principle, the work done by gravity as the particle moves from point A to point B is equal to the change in potential energy:
W=PEB−PEA
- Substituting the values we calculated:
W=0−mgr=−mgr
6. Interpret the Result:
- The negative sign indicates that the work done by gravity is in the direction of the particle's motion (downward).
7. Conclusion:
- The work done by gravity as the particle moves from point A to point B is:
W=mgr
- The particle is released from point A, which is at the top of the hemispherical bowl.
- The lowest point B is at the bottom of the bowl.
- Let the radius of the hemispherical bowl be r. The height h of the particle at point A is equal to the radius r of the bowl, so h=r.
- The potential energy (PE) at point A can be calculated using the formula:
PEA=mgh=mg(r)
- Since h=r, we have:
PEA=mgr
- At point B (the lowest point), the height is 0, so the potential energy at point B is:
PEB=mg(0)=0
- According to the work-energy principle, the work done by gravity as the particle moves from point A to point B is equal to the change in potential energy:
W=PEB−PEA
- Substituting the values we calculated:
W=0−mgr=−mgr
- The negative sign indicates that the work done by gravity is in the direction of the particle's motion (downward).
- The work done by gravity as the particle moves from point A to point B is:
W=mgr
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
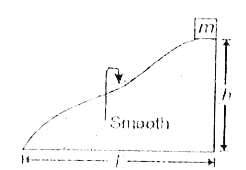
A block of mass m is released along a smooth track shown in figure from its top point. Find the word done by gravity during its downward motion to the bottom of track.
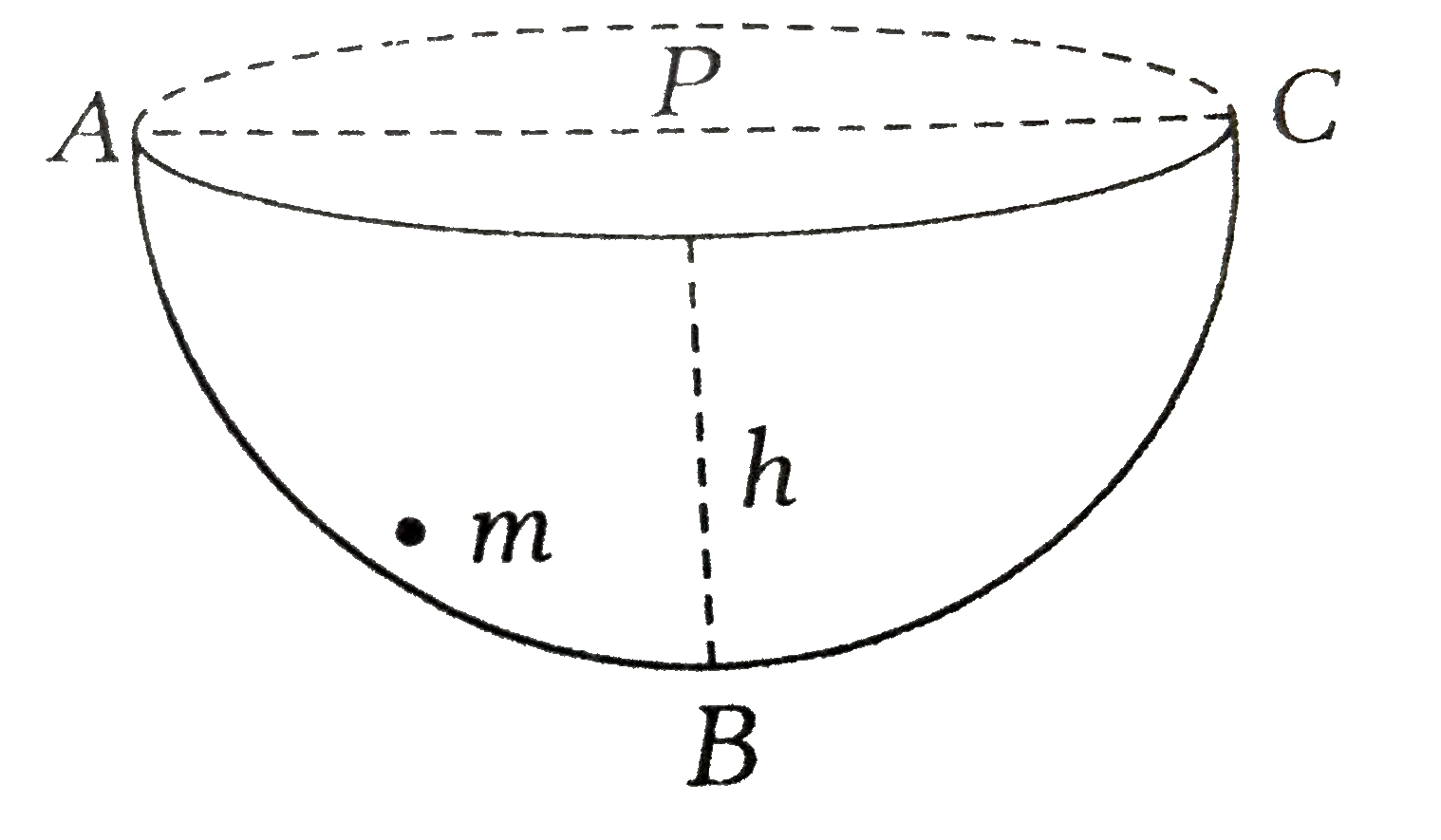
View SolutionA particle of mass m makes SHM in a smooth hemispherical bowl ABC and it moves from A to C and back to A via ABC,so that PB=h. Find the speed of the ball when it just crosses the point B.
View SolutionA particle of mass m is projected with speed u at angle θ with horizontal from ground. The work done by gravity on it during its upward motion is
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
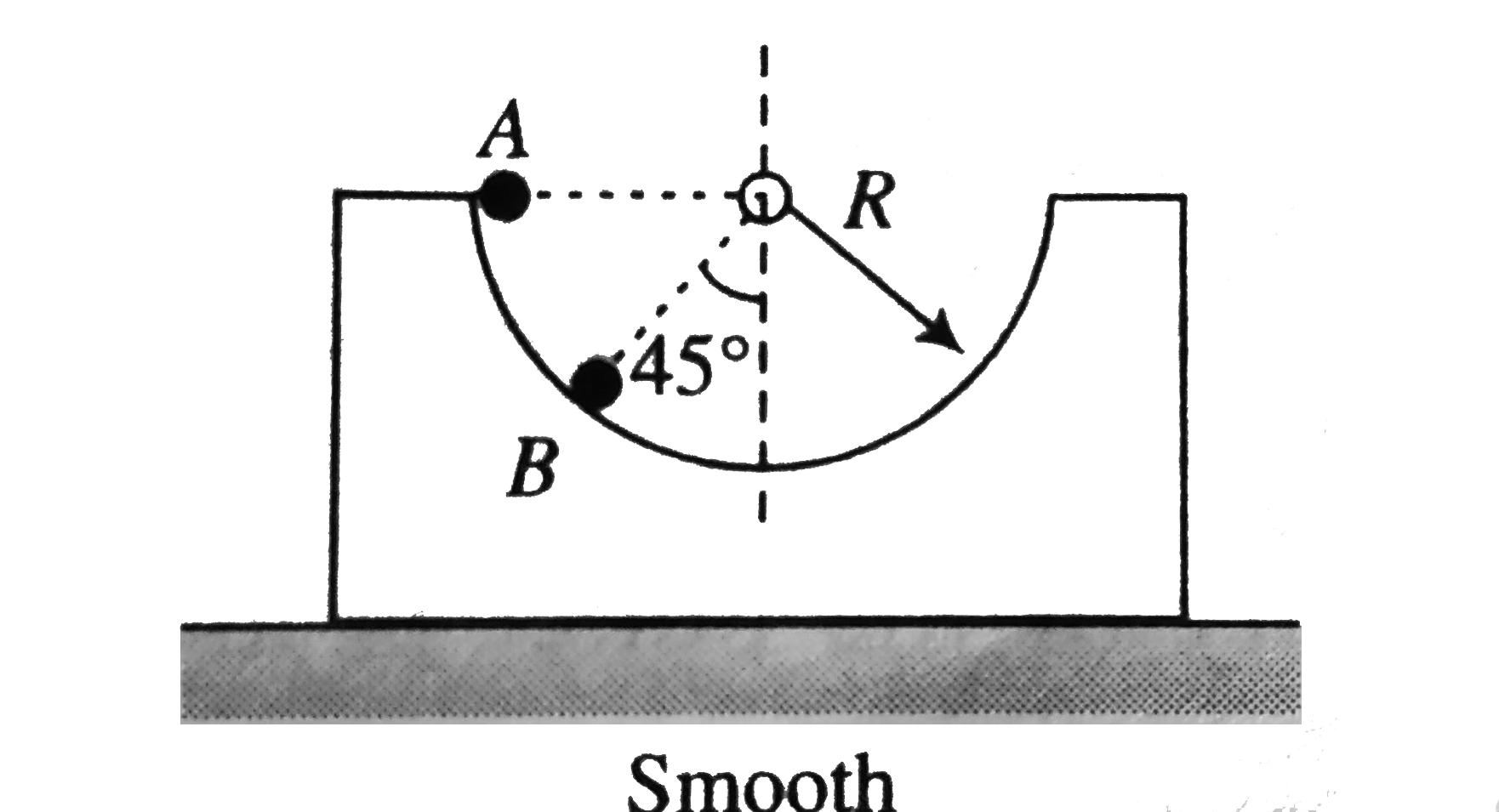
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
View SolutionA particle of mass 'm' is raised from the surface of earth to a height h = 2R. Find work done by some external agent in the process. Here, R is the radius of earth and g the acceleration due to gravity on earth's surface.
View SolutionA particle of mass.m. is projected with a velocity .u. at an angle . θ. with the horizontal. Work done by gravity during its descent from its highest point to a point which is at half the maximum height is
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
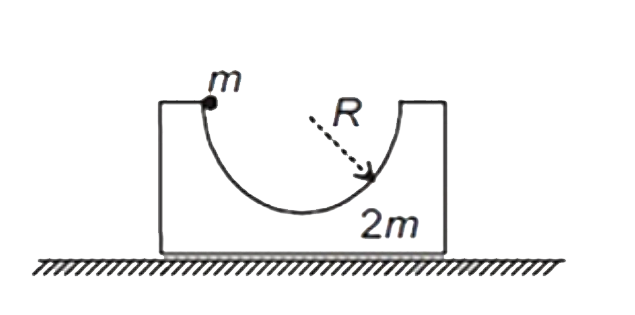
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is

View Solution
