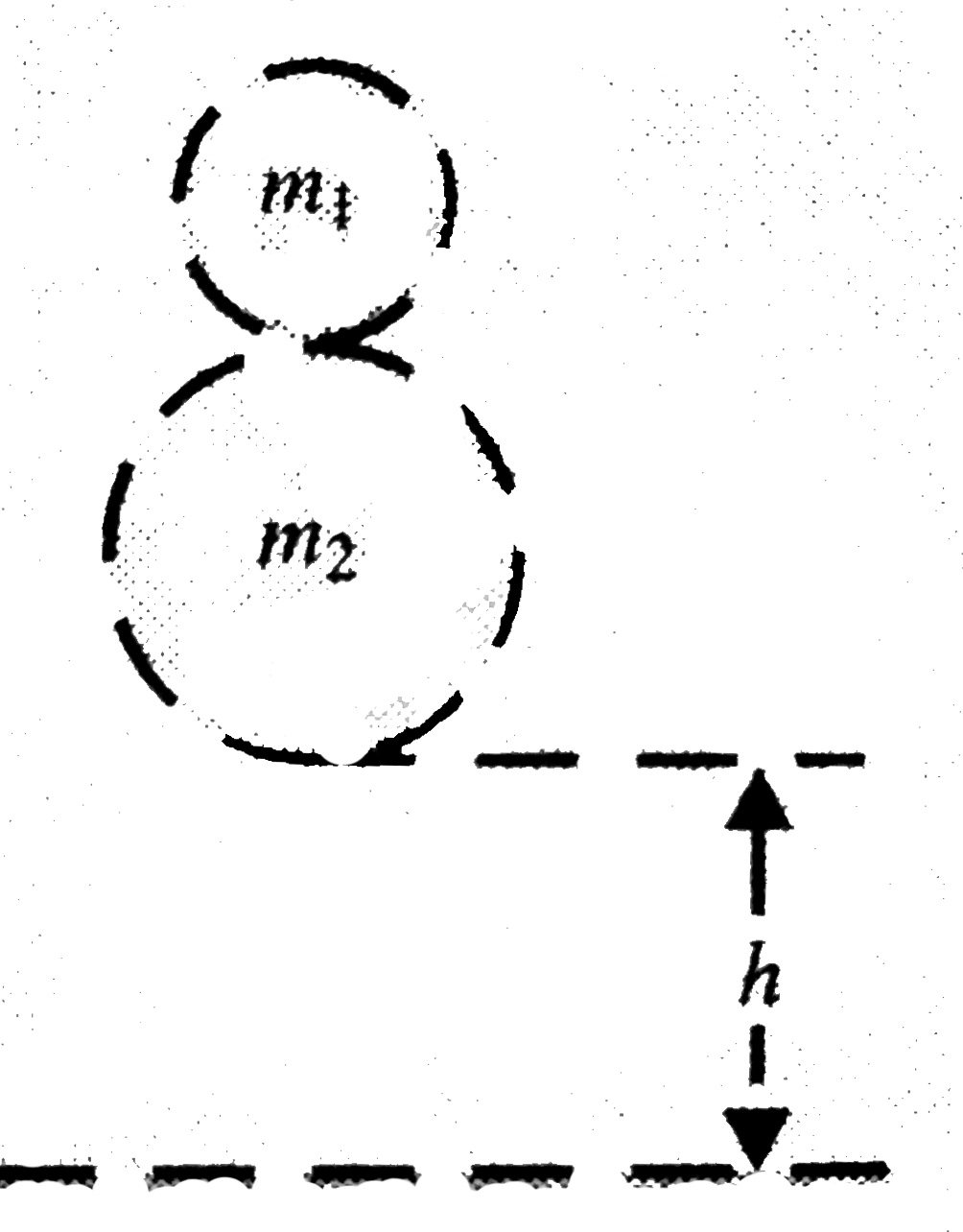
A spring-mass system ( m1 + massless spring + m2) fall freely from a height h before m2 colliding inelastically with the ground. Find the maximum value of h so that block m2 will break off the surface. Assume k=stiffness of the spring.

v1=√2gh

For block m2 to be lifted up
kx=m2g⇒x=m2gk
Now,
12m1v21=m1gx+12kx2
Solve to get h=m2(2m1+m2)g2m1k
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A spring-mass system ( m1 + massless spring + m2) fall freely from a height h before m2 colliding inelastically with the ground. Find the minimum value of h so that block m2 will break off the surface. Assume k=stiffness of the spring.

View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.

View SolutionTwo spherical bodies of mass m1 and m2 fall freely through a distance h. before the body m2 collides with the ground. If the coefficient of restitution of all collisions is e, find the velocity of m1 just after it collides with m2
View SolutionA spring mass system is held at rest with the spring relaxed at a height (H) above the ground. Determine the minimum value of (H) so that the systen has a tendency to rebound after hitting the ground. Given that the coefficient of restitution between (m2) and ground is zero.
 .
.
View SolutionIn the figure shown a massless spring of stiffness k and natural length l0 is rigidly attached to a block of mass m and is in vertical position. A wooden ball of mass m is released from rest to fall under gravity. Having fallen a height h the ball strikes the spring and gets stuck up in the spring at the top. What should be the minimum value of h so that the lower block will just lose contact with the ground later on ? Assume that l0>>4mgk. Neglect any loss of energy. (Given k=mg/2)

View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
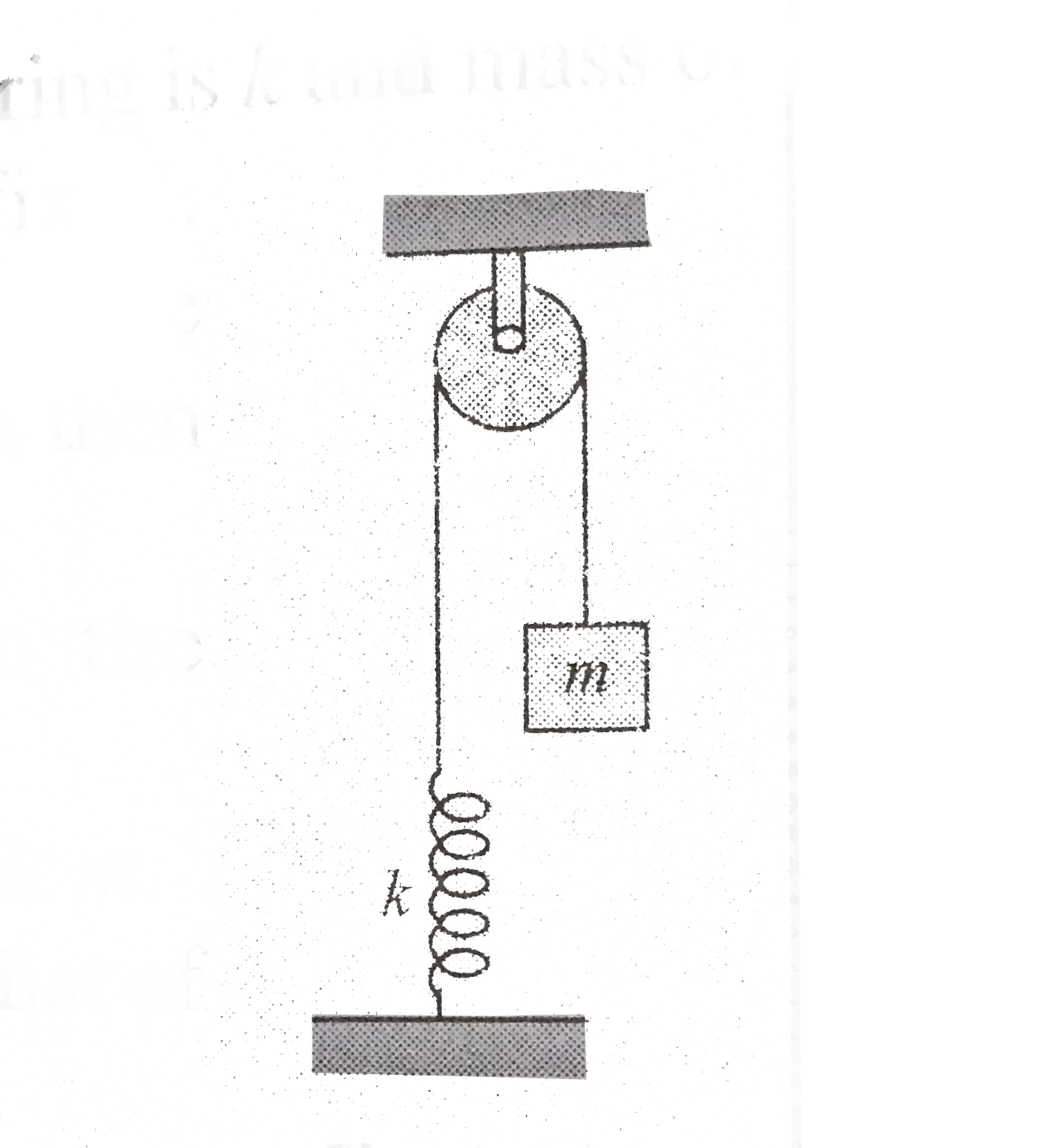
View SolutionA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View Solution
