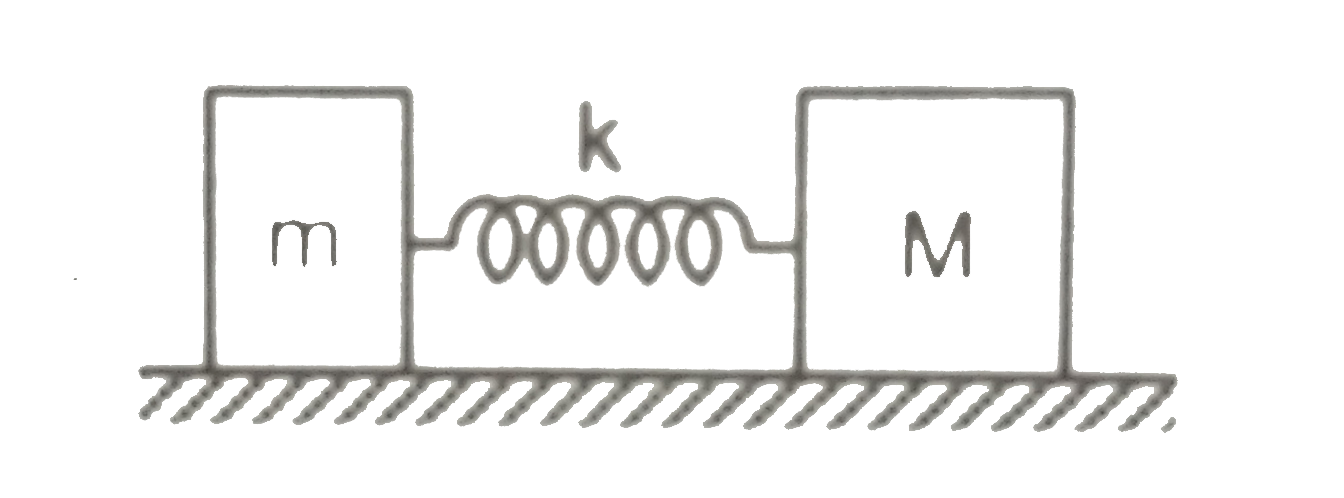
A light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. I fhte spring was initially compressed through a distance d find the final speeds of the two blocks.
 Solution in Gujrati
Solution in Gujrati
Consider the two blocks plus the spring to be the system. No exterN/Al force acts on this system in horizontal direction. Hence, the linear momentum will remain constant. As the spring is light, it has no linear momentum. Suppose the block of mass M moves with a speed V and the other block with a speed v after losing contact with the spring. As the blocks are released from rest the initial momemtum is zero. The fiN/Al momentum is MV−mv towards right. Thus,
MV−mv=0orV=mMv......... i
initially the energy of the system =12kx2.
FiN/Ally, the energy of the system =12mv2+12MV2
As there is no friction
12mv2+12MV2=12kx2....ii
Using i and ii
mv2(1+mM)=kx2
or, v=√kMm(M+m)x
and V=√kmM(M+m)□x
Similar Questions
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. If the spring was initially compressed through a distance d find the final speeds of the two blocks.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA spring of force constant k is kept in the compressesd condition between two blocks masses m and M on the smooth surface of a table as shown in figure .When the spring is released , both the blocks move in opposite directions .When the spring attains the orginal (normal ) position . both blocks lose the constacts with the spring . If x is the intial compression of the spring find the speeds of block while getting detached from the spring .
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA block of mass m is pushed up against a spring, compressing it a distance x, and the block is then released. The spring projects the block along a frictionaless horizontal surface, grving the block a speed v. The same spring projects a second block of mass 4m, giving it a speed 3v. What distance was the spring compressed in the second case ?
View Solution