A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
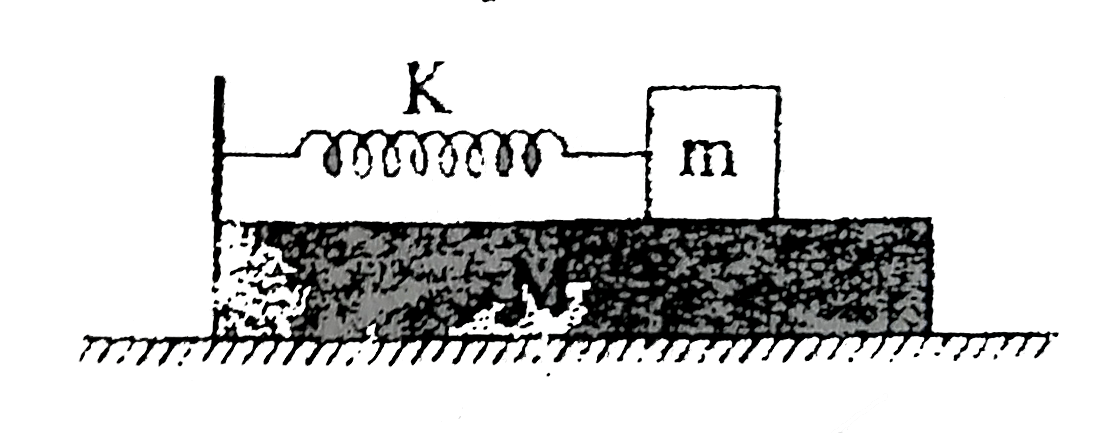
√m2KV0
√mKv0
√2mKv0
2√mKv0
The correct Answer is:A
Compression will be maximum when relative velocity between blocks is zero.
Means both have Sam velocity apply conservation of momentum
mv0=(M+m)v
⇒v=mM+mv0
Apply conservation of kinetic energy
12mv2+12Mv2+12kx2=12mv20
⇒m3v20(M+m)2+m2Mv20(M+m)2+kx2=mv20
⇒kx2=m3+m2M(M+m)2v20=mv20
⇒kx2=v20[mp−m2(M+m)(M+m)2]
=v20[Mm+m2−m2M+m]=Mmv20M+m
⇒x=√Mmk(M+m)v0
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
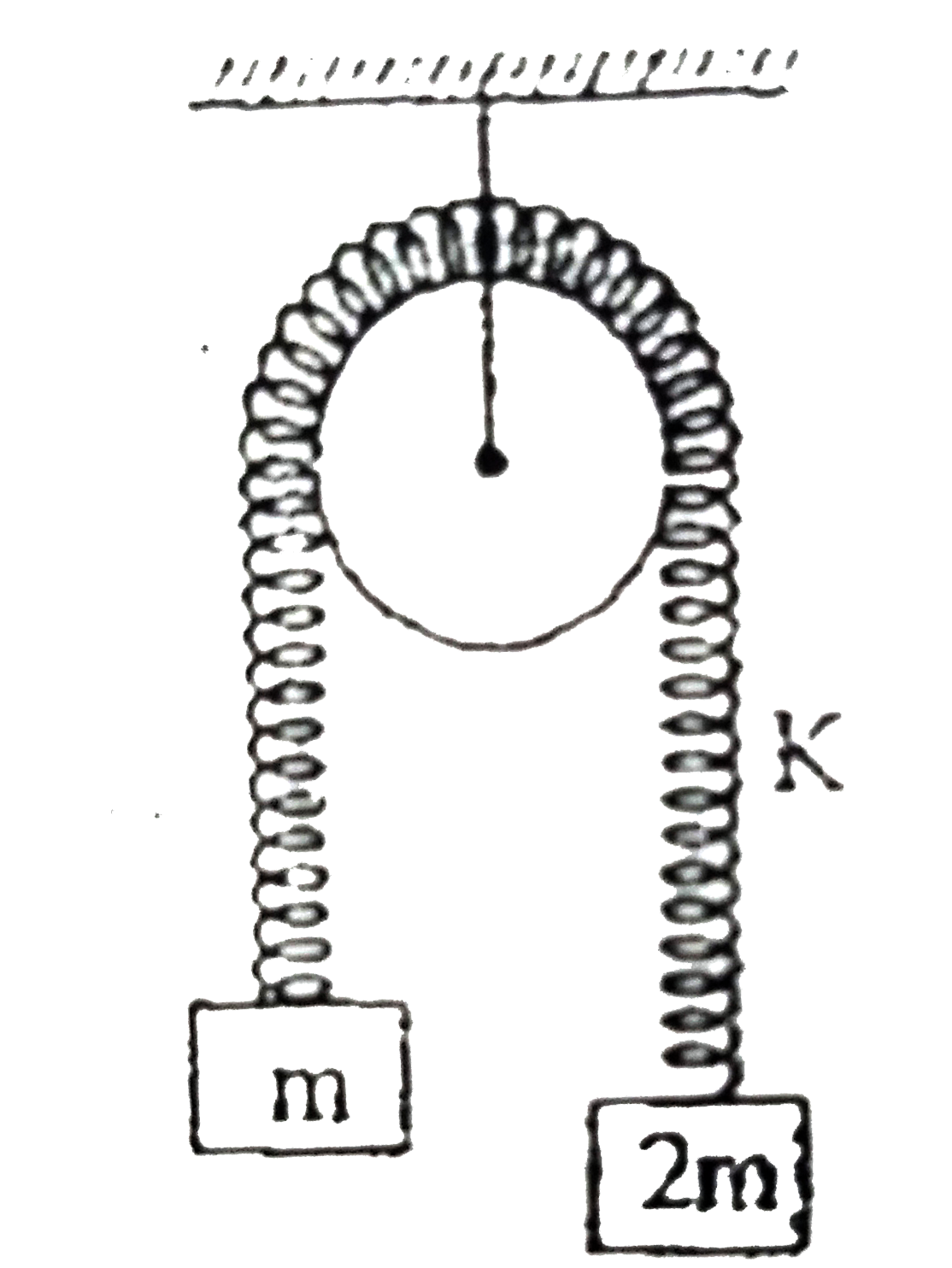
Two blocks of mass m and 2m are connected to a spring and wrapped around a smooth pulley as shown in the figure. Blocks are released together with spring in natural length. Calculate the maximum elongation (in meter) of the spring. Given mgK=3 meter.
View SolutionBlock of mass m is pushed towards a horizontal spring as shown in figure , with initial speed u .

Spring constant of the spring is K and floor is smooth . Calculate maximum possible compression of the spring .
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
 Aπ2√MkB2π√M5kC3π2√MkDπ√M2k
Aπ2√MkB2π√M5kC3π2√MkDπ√M2k
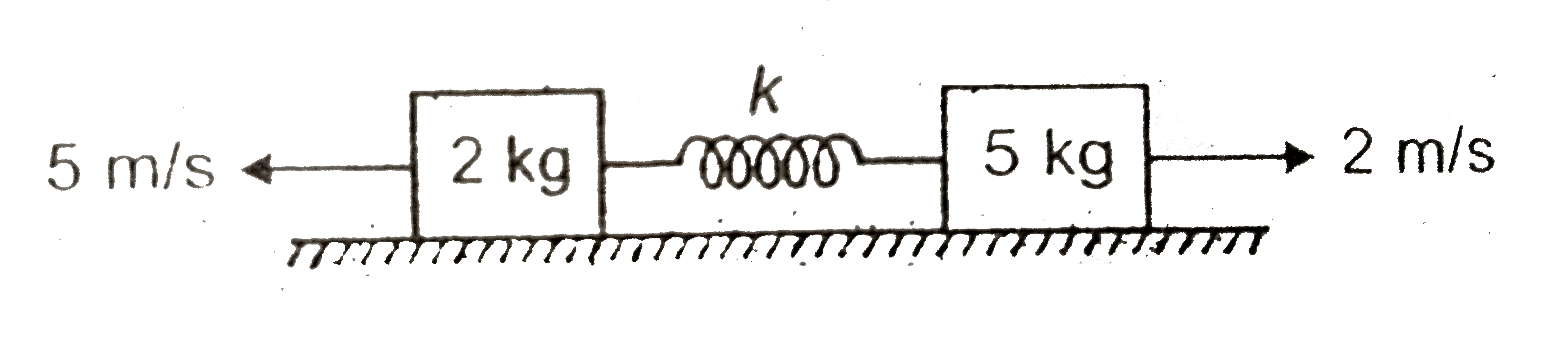
Two blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring

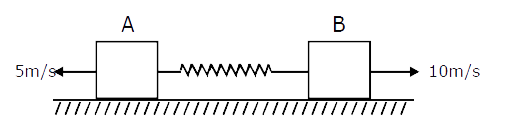
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View Solution

