A rotor is rotating with a constant angular velocity ω about its own axis. At the centre of the rotaor a spring is fixed of natural length (l0) whose other end is connected to a block of mass m. Find the minimum vaule of coefficient of friction between block and rotor wall for which spring remains horizontal. The radius of rotor is R(R<l0).
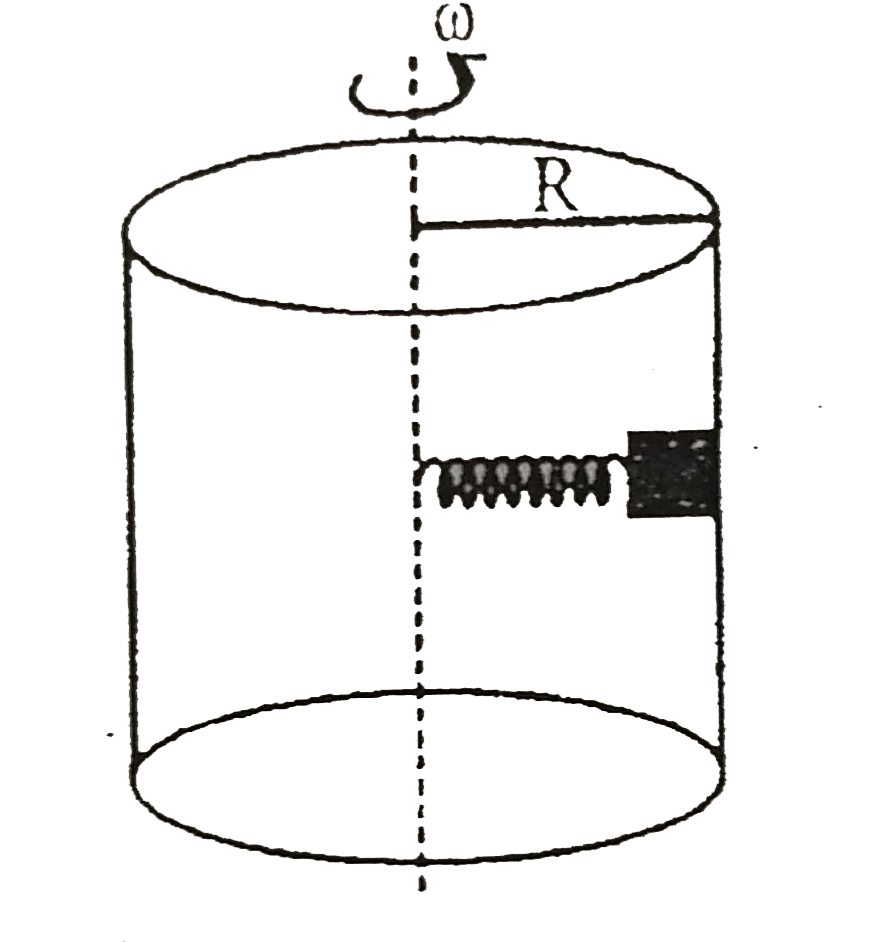
μ=mgmω2R+K(l0−R)
μ=mgK(l0−R)
μ=mgmω2R−K(l0−R)
μ=mgKR
The correct Answer is:A
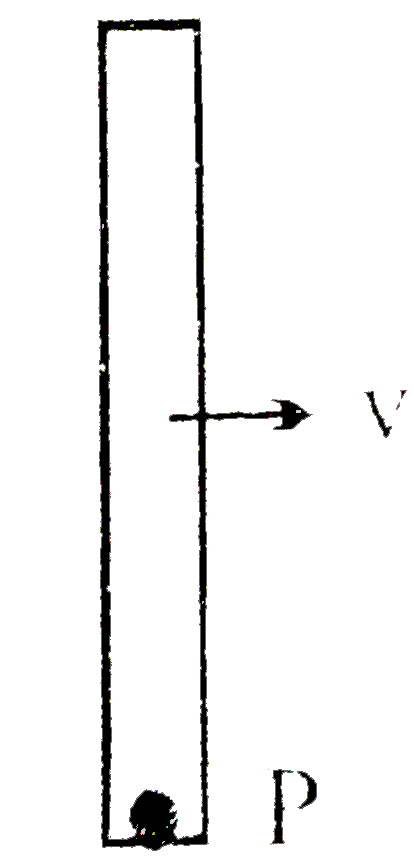
−kΔx+N=mRω2
Δx=l0−R
−k(l0−R)+N=mRω2
N=mRω2+k(l0−R)
f=μN=mg
μ=mgN
μ=mgmRω2+k(l0−R)
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
One end of a light spring constant k and natural length l0 is fixed and the other end is attached to a block of mass m lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius l, find the frequency of the revolution.
View SolutionTwo small blocks of mass mA=30 kg & mB =15 kg are connected with spring & kept on the wedge which is rotating about given axis as shown in figure. If blocks B remain in rest then minimum value of coefficient of friction between block A & wedge is μ0, then the value of μ20 is :
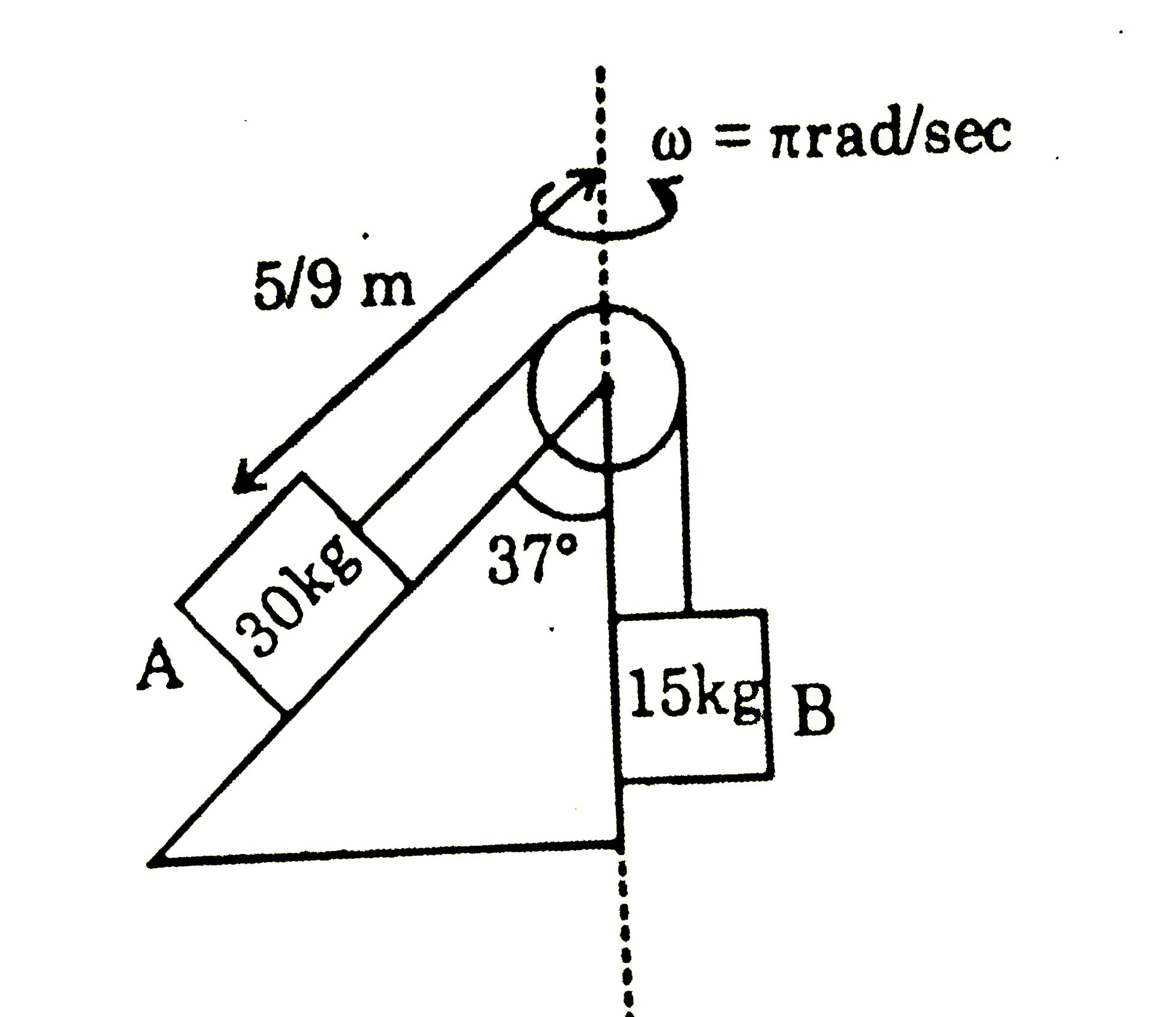
View Solution
Knowledge Check
A rotor is rotating with a constant angular velocity ω about its own axis. At the centre of the rotor a spring is fixed of nature length (l0) whose other end is connected to a block of mass m. Find the minimum value of coefficient of friction between block and rotor wall for which spring remains horizontal. The radius of rotor is R(R>l0).
 Amgmω2R+K(R−l0)Bmgmω2R−K(R−l0)Cmg(mω2+K)RDmg(mω2−K)R
Amgmω2R+K(R−l0)Bmgmω2R−K(R−l0)Cmg(mω2+K)RDmg(mω2−K)RA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
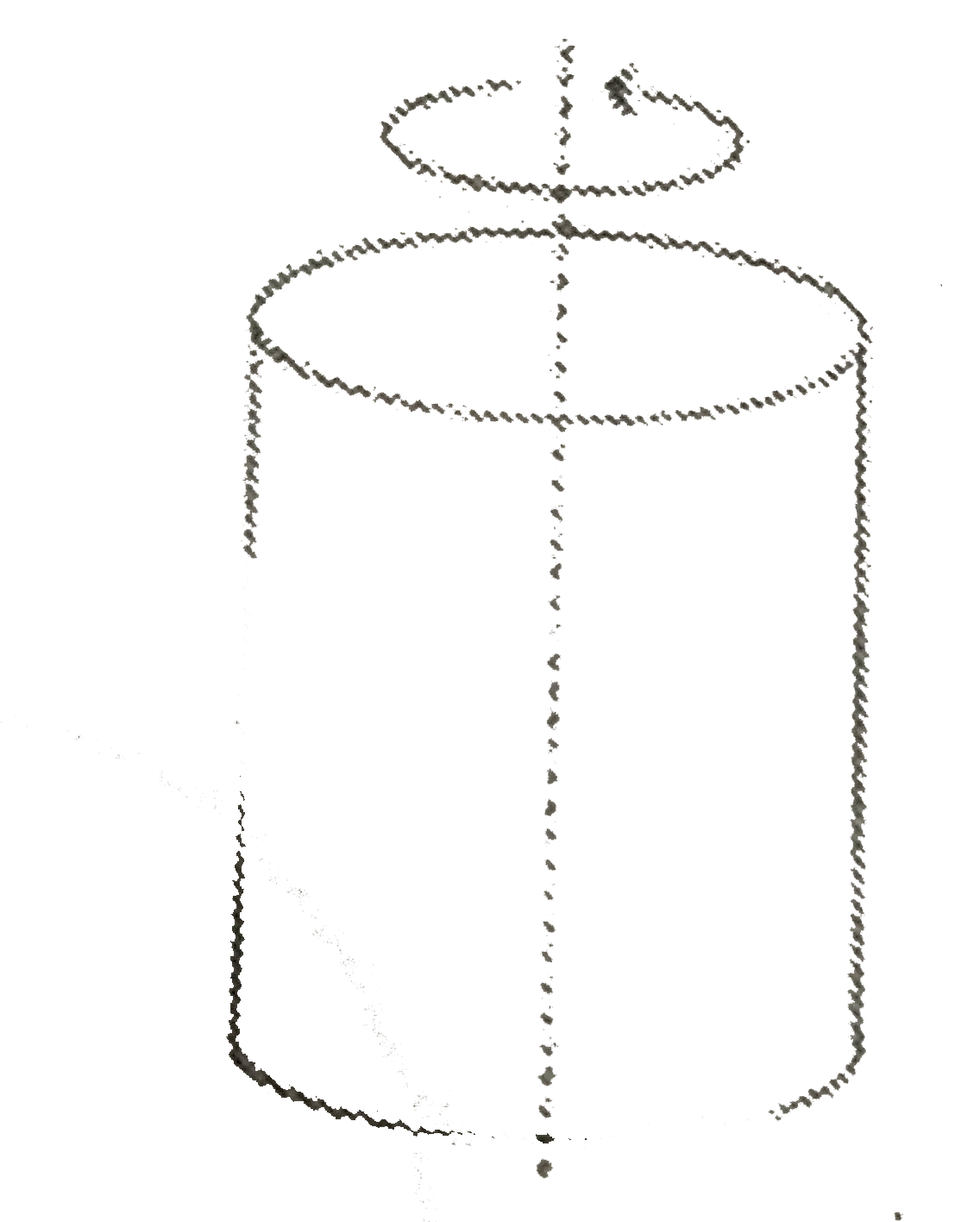 Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R
Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R
A block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
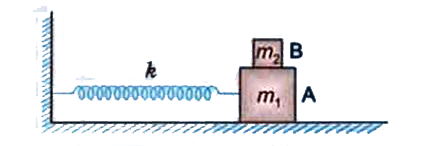
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
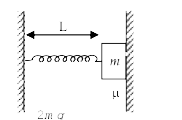
View SolutionA block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View Solution

