The S-shaped unifrom wire shown in figure has a mass M, and the radius of curvature of each half is R. The moment of inertia about an axis through A and perpendicular to the plane of the paper is:

34MR2
MR2
32MR2
2MR2
The correct Answer is:D
In the plane
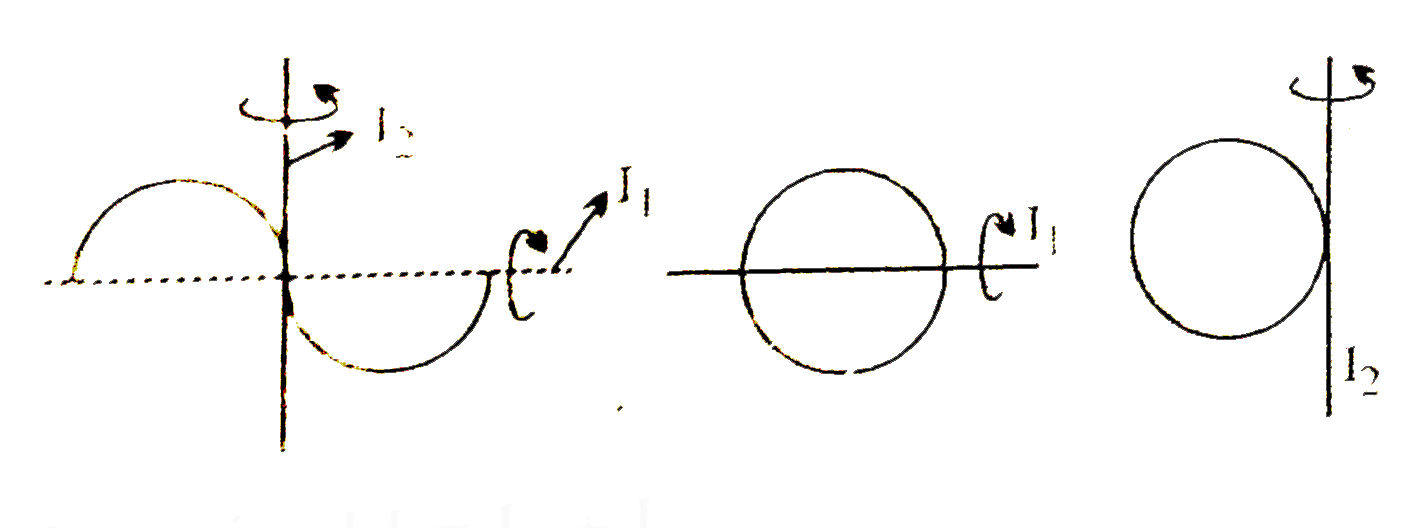
Required I=I1+I2
∴I1=MR22 & I2=MR22+MR2
∴I=2MR2
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View Solution
Knowledge Check
A disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
A12m(R−r)2B12m(R2−r2)C12m(R+r)2D12m(R2+r2)In the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
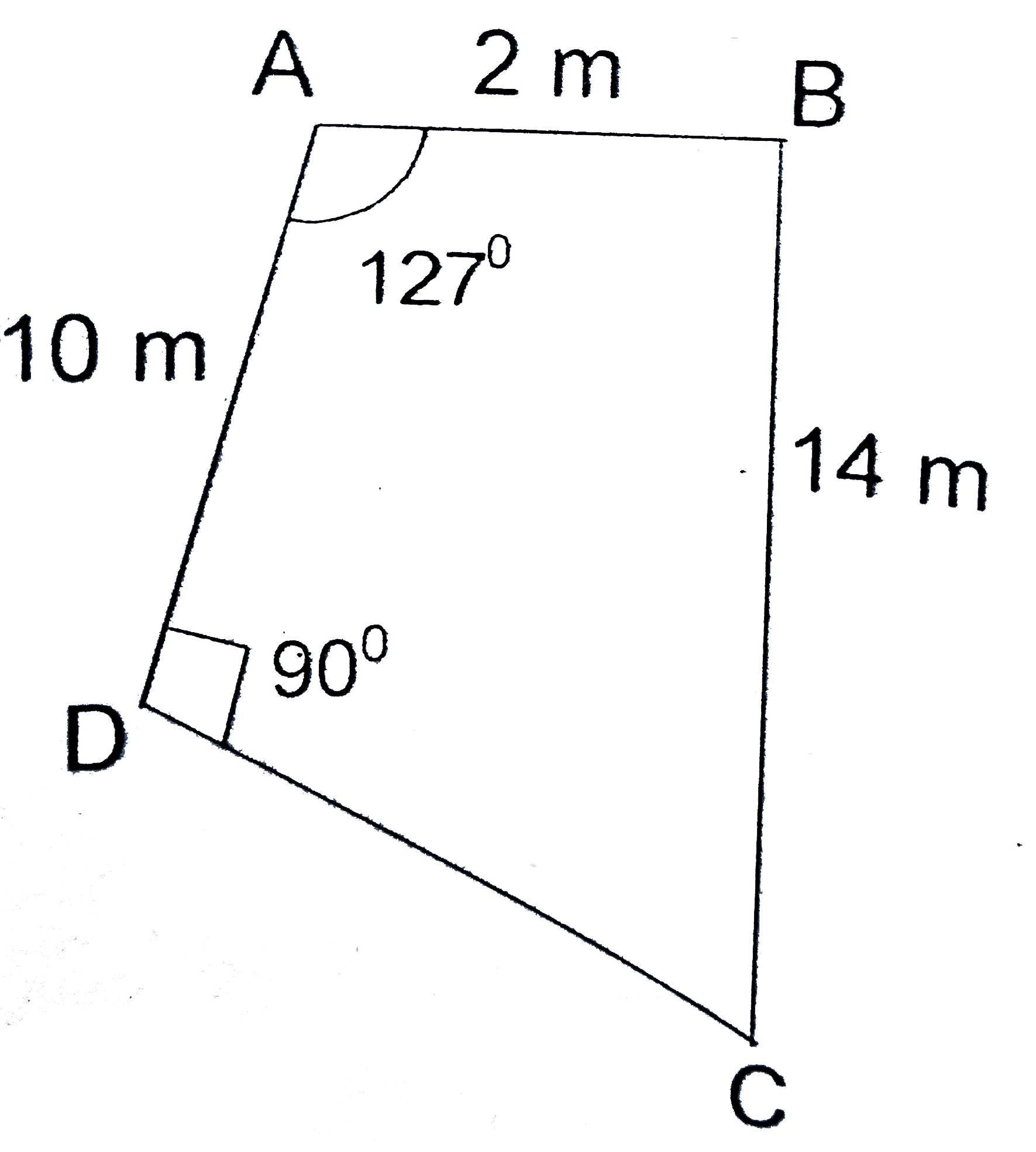 A256kgm2B512kgm2C200kgm2D100kgm2
A256kgm2B512kgm2C200kgm2D100kgm2The diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
 A43Ma2BI+14Ma2C2IDI2
A43Ma2BI+14Ma2C2IDI2
(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure (a) through (f)) to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is I0=12MR2 where M= mass of the fan.

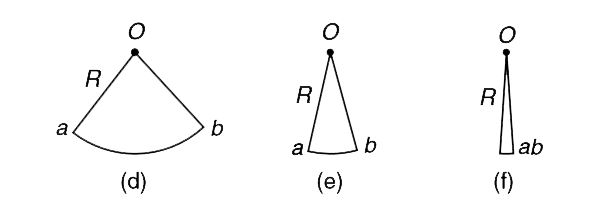
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. (f)), write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is ML23
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View Solution

