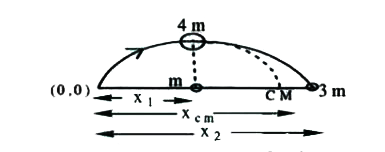
A projectile is fired at a speed of 100m/s at an angle of 37∘ above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the point where the heavier piece lands.
Internal forces do not affect the motion of the centre of mass, the centre of mass hits the ground at a position where the original projectile would have landed. The range of the original projectile is
XCM=2u2sinθcosθg=2×104×35×4510m=960m
The centre of mass will hit the ground at this position. As the smaller block comes to rest after breaking, it falls down vertically and hits the ground at half of the range, i.e., at x = 480 m. If the heavier block hits the ground at x2, then
XCM=m1x1+m2x2m1+m2⇒960=(m)(480)+(3m)(x2)(m+3m)
∴x2=1120m
Similar Questions
A projectile is fired at a speed of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
 View Solution
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass 5 kg is projecte with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. At the highest point of its path , the projectile explodes and breaks up into two fragments of masses 1kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that K.E. of the system at the highest point is doubled. Calculate the separation betweent the two fragments when they reach the ground.
A11 mB22 mC44 mD66 m
A projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA projectile is fired from level ground at an angle θ above the horizontal. The elevation angle ϕ of the highest point as seen from the launch point is related to θ by the relation.
View SolutionA projectile is fired from level ground at an angle θ above the horizontal. The elevation angle ϕ of the highest point as seen from the launch point is related to θ by the relation.
View SolutionA projectile of mass 3kg is projected with velocity 50m/s at 37∘ from horizontal. After 2s, explosion takes place and the projectile breaks into two parts of masses 1kg and 2kg. The first part comes to rest just after explosion.
Find,
(a) the velocity of second part just after explosion.
(b) maximum height attained by this part. Take g=10m/s2View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
(A)43R (B)32R (C)54R (D)2.5RView SolutionA shell is fired from a cannon with a speed of 100m/s at an angle 30∘with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1:2. The lighter fragment moves vertically upwards with an initial speed of 200m/s. What is the speed of the heavier fragment at the time of explosion?
View Solution
