A projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance from point of firing) of the lighter part is:
16 km
1 km
10 km
2 km
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of the projectile before and after the explosion.
Step 1: Understand the Initial Conditions
The projectile is fired with a horizontal range of 4 km. This means that the total horizontal distance covered by the projectile before it hits the ground is 4 km.
Step 2: Determine the Velocity at the Highest Point
At the highest point of its trajectory, the vertical component of the velocity is zero, and the horizontal component remains constant. The horizontal velocity Vx at the highest point is given by:
Vx=ucosθ
where u is the initial speed and θ is the angle of projection.
Step 3: Apply Conservation of Momentum at the Explosion
When the projectile explodes at the highest point, it splits into two parts with masses M4 and 3M4. The heavier part (mass 3M4) falls vertically with zero initial speed. According to the conservation of momentum, the horizontal momentum before the explosion must equal the horizontal momentum after the explosion.
Before the explosion:
Initial momentum=M⋅Vx=M⋅ucosθ
After the explosion:
Final momentum=3M4⋅0+M4⋅V′
where V′ is the horizontal velocity of the lighter part after the explosion.
Setting the initial momentum equal to the final momentum:
M⋅ucosθ=M4⋅V′
Step 4: Solve for V′
Cancelling M from both sides and solving for V′:
ucosθ=14V′
V′=4ucosθ
Step 5: Calculate the Time of Free Fall for the Heavier Part
The time taken for the heavier part to fall from the maximum height to the ground can be calculated using the formula for free fall:
H=u2sin2θ2g
The time t to fall this height is given by:
H=12gt2
Setting the two expressions for height equal gives:
u2sin2θ2g=12gt2
Solving for t:
t=usinθg
Step 6: Calculate the Horizontal Range of the Lighter Part
The horizontal distance X′ traveled by the lighter part after the explosion can be calculated as:
X′=V′⋅t
Substituting V′ and t:
X′=(4ucosθ)⋅(usinθg)
X′=4u2sinθcosθg
Using the identity sin2θ=2sinθcosθ:
X′=2u2sin2θg
Step 7: Relate to the Range of the Projectile
The horizontal range R of the projectile is given by:
R=u2sin2θg
Thus, we can express X′ in terms of R:
X′=2R
Step 8: Total Horizontal Distance from the Firing Point
The total horizontal distance from the firing point for the lighter part is the sum of the distance traveled before the explosion (which is half the range) and the distance traveled after the explosion:
Total Distance=R2+X′=R2+2R=R2+2R=R2+4R2=5R2
Given R=4 km:
Total Distance=5×42=10 km
Final Answer
The horizontal range of the lighter part is 10 km.
---
The projectile is fired with a horizontal range of 4 km. This means that the total horizontal distance covered by the projectile before it hits the ground is 4 km.
At the highest point of its trajectory, the vertical component of the velocity is zero, and the horizontal component remains constant. The horizontal velocity Vx at the highest point is given by:
Vx=ucosθ
where u is the initial speed and θ is the angle of projection.
When the projectile explodes at the highest point, it splits into two parts with masses M4 and 3M4. The heavier part (mass 3M4) falls vertically with zero initial speed. According to the conservation of momentum, the horizontal momentum before the explosion must equal the horizontal momentum after the explosion.
Initial momentum=M⋅Vx=M⋅ucosθ
Final momentum=3M4⋅0+M4⋅V′
where V′ is the horizontal velocity of the lighter part after the explosion.
M⋅ucosθ=M4⋅V′
Cancelling M from both sides and solving for V′:
ucosθ=14V′
V′=4ucosθ
The time taken for the heavier part to fall from the maximum height to the ground can be calculated using the formula for free fall:
H=u2sin2θ2g
The time t to fall this height is given by:
H=12gt2
Setting the two expressions for height equal gives:
u2sin2θ2g=12gt2
Solving for t:
t=usinθg
The horizontal distance X′ traveled by the lighter part after the explosion can be calculated as:
X′=V′⋅t
Substituting V′ and t:
X′=(4ucosθ)⋅(usinθg)
X′=4u2sinθcosθg
Using the identity sin2θ=2sinθcosθ:
X′=2u2sin2θg
The horizontal range R of the projectile is given by:
R=u2sin2θg
Thus, we can express X′ in terms of R:
X′=2R
The total horizontal distance from the firing point for the lighter part is the sum of the distance traveled before the explosion (which is half the range) and the distance traveled after the explosion:
Total Distance=R2+X′=R2+2R=R2+2R=R2+4R2=5R2
Given R=4 km:
Total Distance=5×42=10 km
The horizontal range of the lighter part is 10 km.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 5: Circular Motion and Banking of Road )
7 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
A 24−kg projectile is fired at an angle of 53∘ above the horizontal with an initial speed of 50m/s. At the highest point in its trajectory, the projectile explodes into two fragments of equal mass, the first of which falls vertically with zero initial speed.
(a) How far from the point of firing does the second fragment strike the ground? (Assume the ground is level.)
(b) How much energy was released during the explosion?
View SolutionA projectile of mass mis fired with an initial velocity v0 at an angle 0 to the horizontal. At its highest point, it explodes into two fragments of equal mass. One of the fragments falls vertically with zero initial speed. Since the only external force acting on the system is gravitational, the motion of centre of mass of the_ system (the fragments) follows the same parabolic path as the projectile would have followed if there had been no explosion. Force of explosion is internal, it cannot change the trajectory of the system.

View Solution
Knowledge Check
A projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
A24000 mB16000 mC32000 mD8000 mA particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of theseA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
A3R4B3R2C5R4D3R
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
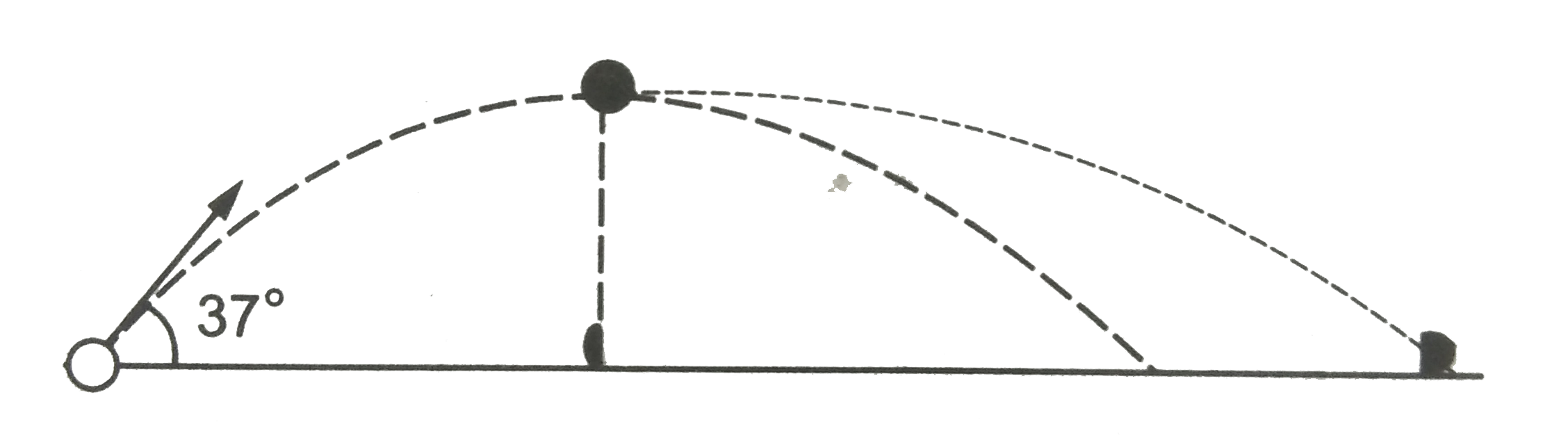
View SolutionA projectile is fired with velocity u at an angle θ with horizontal. At the highest point of its trajectory, it splits up into three segments of masses m, m and 2m. First part falls vertically downward with zero initial velocity and second part returns via same path to the point of projection. The velocity of third part of mass 2 m just after explosion will be
View SolutionA body of mass m is projected from ground for horizontal range R. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
View SolutionA projectile is fired from horizontal at an angle θ . What are the horizontal and vertical acceleration at the highest point ?
View Solution
