A bomb of mass 4m, while moving on a parabolic path, explodes at highest point of its path. If breaks into two parts of mass ratio 1:3, smaller part coming to rest. The range of this projectile was 60m in the absence of explosion. The distance of the second part from the point of projection when it strikes the ground is
60m
70m
80m
90m
The correct Answer is:B
At the highest point , the bomb has horizontal velocity . The smaller part comes to rest, hence the larger part will move with higher horizontal velocity (due to the momentum conservation in horizontal direction)
4mv0=m×0+3mv⇒v>v0
In the vertical direction , both parts have no velocity , hence both will strike the ground simultaneously.
As the internal forces do not affect the motion of the center of mass , the center of mass hits the ground at the position where the original bomb (projectile) would have landed.
xc.m.=R=m×R2+3mx0m+3m⇒x0=70m

Topper's Solved these Questions
Similar Questions
A projectile of mass 3m explodes at highest point of its path. It breaks into three equalparts. One part retraces its path, the second one comes to rest. The range of the projectile was 100 m if no explosion would have taken place. The distance of the third part from the point of projection when it finally lands on the ground is -
View SolutionA body is projected with a speed 160 m/s at an angle 53∘ with the horizontal, At the highest point, body explodes into two pieces with mass ratio 1:3. Smaller piece comes to rest immediately after explosion. Find the distance of point from point of projection where heavier piece strikes the horizontal surface.
View Solution
Knowledge Check
A projectile of mass 3m explodes at highest point of its path. It breaks into three equalparts. One part retraces its path, the second one comes to rest. The range of the projectile was 100 m if no explosion would have taken place. The distance of the third part from the point of projection when it finally lands on the ground is -
A100mB150mC250mD300mIn the previous problem , if a bomb explodes into three parts of mass ratio 1:1:2 , one smaller part retraces its path, the second smaller part coming to rest, the distance from the point of projection , where the heavier part strikes the ground is
A75mB95mC105mD120mA particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of these
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View SolutionA particle is moving along x-axis with velocity 40 m/s. It breaks into two parts in mass ratio 1:2. If speed of smaller part is 60 m/s along x-axis then find fractional changes in kinetic energy of system.
View SolutionOne projectile moving with velocity v in space, gets burst into 2 parts of masses in the ratio 1:3. The smaller part becomes stationary. What is the velocity of thhe other part?
View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
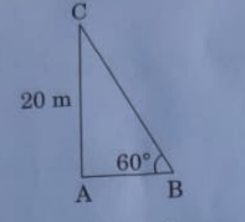
View Solution

