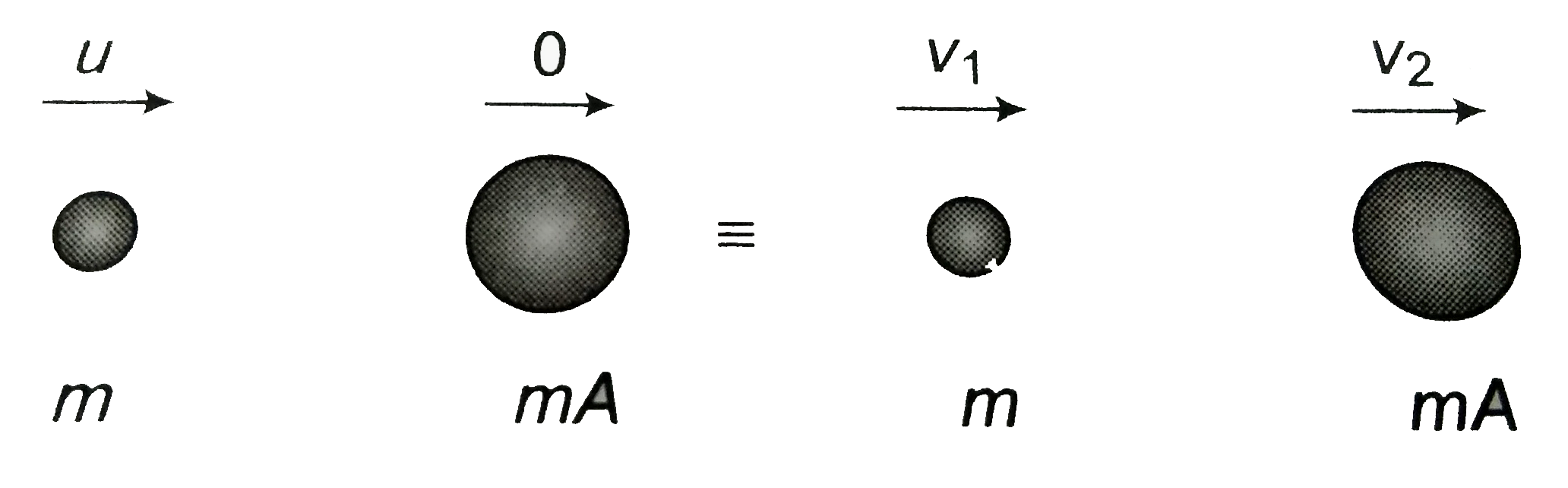
A neutron collides head-on and elasticity with an atom of mass number A, which is initially at rest. The fraction of kinetic energy retained by neutron is
(AA+1)2
(A−1A+1)2
(A−1A)2
(A+1A−1)2
The correct Answer is:B
μ=mv1+mAv2 (i)
v1+u=v2+0 (ii)
v1=(1−A1+A)u
Fraction of energy retained by neutron is
⎛⎝12mv2112μ2⎞⎠=(v1u)2=(1−A1+A)2=(A−1A+1)2
Topper's Solved these Questions
Similar Questions
A neutron travelling with a velocity v and kinetic energy E collides head-on elastically with a nucleus of mass number A at rest. Calculate the fraction of total energy retained by the neutron.
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View Solution
Knowledge Check
A neutron travelling with a velocity v and kinetic energy E collides elastically head on with the nucleus of an atom of mass number A at rest. The fraction of total energy retained by the neutron is :
A(A−1A+1)2B(A+1A−1)2C(A−1A)2D(A+1A)2A neutron in a nuclear reactor collides head on elastically with the nucleus of a carbon atom initially at rest. The fraction of kinetic energy transferred from the neutron to the carbon atom is
A1112B211C48121D48169A neutron travelling with a velocity v and kinetic energy E collides perfectly elastically head on with the nucleus of an atom of mass number A at rest. The fraction of the total kinetic energy retained by the neutron is
A(A−1A+1)2B(A+1A−1)2C(A−1A)2D(A+1A)2
A body of mass m moving with velocity v collides head-on elastically with another body of mass 2m which is initially at rest. The ratio of K. E. of mass m before and after the collision will be
View SolutionA neutron moving at a speed v undergoes a head-on elastic collision with a nucleus of mass number A at rest. The ratio of the kinetic energies of the neutron after and before collision is :
View SolutionA neutron travelling with a velocity v and kinetic energy E collides perfectly elastically head on with the nucleus of an atom of mass number A at rest. The fraction of the total kinetic energy retained by the neutron is
View SolutionA neutron collides head-on and elasticity with an atom of mass number A, which is initially at rest. The fraction of kinetic energy retained by neutron is
View SolutionA ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
View Solution
