The velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
v1=v1(V1V2)
v1=v1(V2V1)
v1=v1√V2V1
v1=v1√V1V2
The correct Answer is:B
To solve the problem, we need to establish the relationship between the velocities of sound in an ideal gas and the root mean square (RMS) velocities of the gas molecules at two different temperatures T1 and T2.
1. Understanding the Formulas:
- The RMS velocity of gas molecules at temperature T is given by:
vRMS=√3RTM
where R is the universal gas constant and M is the molecular mass of the gas.
- The velocity of sound in an ideal gas at temperature T is given by:
Vs=√γRTM
where γ=CpCv is the ratio of specific heats.
2. Establishing Proportional Relationships:
- From the formulas, we can see that both vRMS and Vs are directly proportional to √T:
vRMS∝√TandVs∝√T
3. Setting Up the Ratios:
- For two different temperatures T1 and T2, we can write the ratios:
vRMS1V1=vRMS2V2
4. Substituting Known Values:
- It is given that vRMS1=V1 and vRMS2=V2. Therefore, we can substitute these into the ratio:
V1V1=V2V2
- This simplifies to:
1=1
- This indicates a consistent relationship.
5. Final Relationship:
- Rearranging the ratio gives us:
V1vRMS1=V2vRMS2
- From this, we can express vRMS2 in terms of vRMS1:
vRMS2=vRMS1⋅V2V1
Final Answer:
Thus, the relationship can be summarized as:
vRMS2=vRMS1⋅V2V1
- The RMS velocity of gas molecules at temperature T is given by:
vRMS=√3RTM
where R is the universal gas constant and M is the molecular mass of the gas.
- The velocity of sound in an ideal gas at temperature T is given by:
Vs=√γRTM
where γ=CpCv is the ratio of specific heats.
- From the formulas, we can see that both vRMS and Vs are directly proportional to √T:
vRMS∝√TandVs∝√T
- For two different temperatures T1 and T2, we can write the ratios:
vRMS1V1=vRMS2V2
- It is given that vRMS1=V1 and vRMS2=V2. Therefore, we can substitute these into the ratio:
V1V1=V2V2
- This simplifies to:
1=1
- This indicates a consistent relationship.
- Rearranging the ratio gives us:
V1vRMS1=V2vRMS2
- From this, we can express vRMS2 in terms of vRMS1:
vRMS2=vRMS1⋅V2V1
Thus, the relationship can be summarized as:
vRMS2=vRMS1⋅V2V1
Topper's Solved these Questions
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Pipes)
Explore 13 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Beats : )
Explore 20 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Strings (Speed of a travelling wave:))
Explore 23 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:PROBLEMS (LEVEL - II)
Explore 33 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -III (POLARISITION)
Explore 10 Videos
Similar Questions
Knowledge Check
Assertion : Current versus potential difference (i-V) graph for a conductor at two different temperatures T1 and T2 is shown in figure. Hence T1>T2.

Reason : Resistance of a conductor increases with rise in temperature.Acos2θBsin2θCcot2θDtan2θ
Two bodies of masses (m1) and (m2) are droppded from heithts h1 and h2, respectively. They reach the ground after time t1 and t2 and strike the ground with v1 and v2, respectively Choose the correct relations from the following.
View SolutionThe area of hole (1) is A1 and of hole (2) is A2. The velocity of efflux and range of liquid is v1,v2andx1,x2 for holes (1) and (2) respectively. The time taken by liquid, jet to reach the ground from holes (1) and (2) are t1andt2 respectively. Cross section of tank is very very large compared to size of holes.
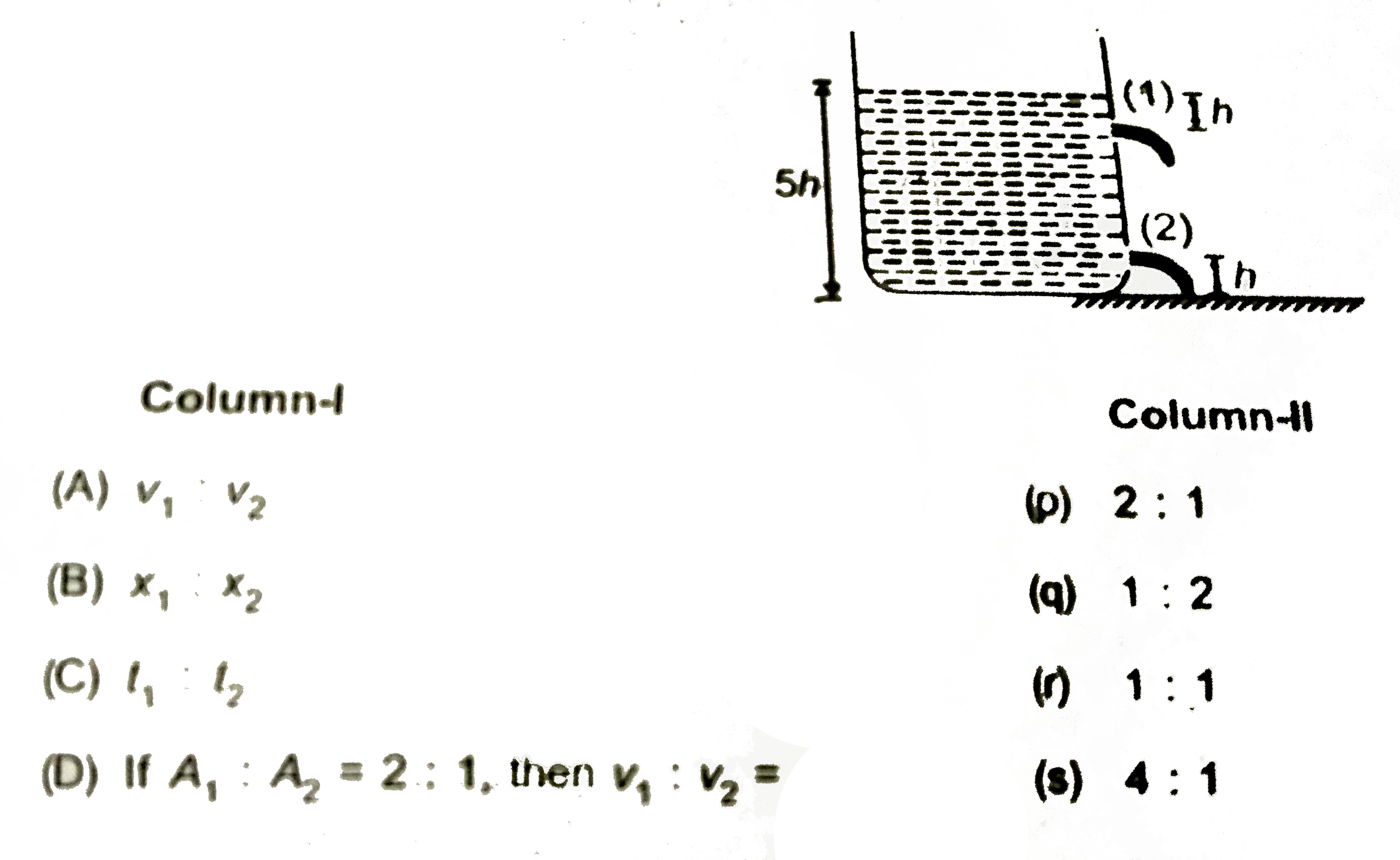
Column-IColumn-II(A)v1:v2(p)2:1(B)x1:x2(q)1:2(C)t1:t2(r)1:1(D)ifA1:A2=2:1,thenv1:v2=(s)4:1
View SolutionThree isothermal plots (P versus V) A, B and C are plotted at three temperature T1,T2andT3 respectively
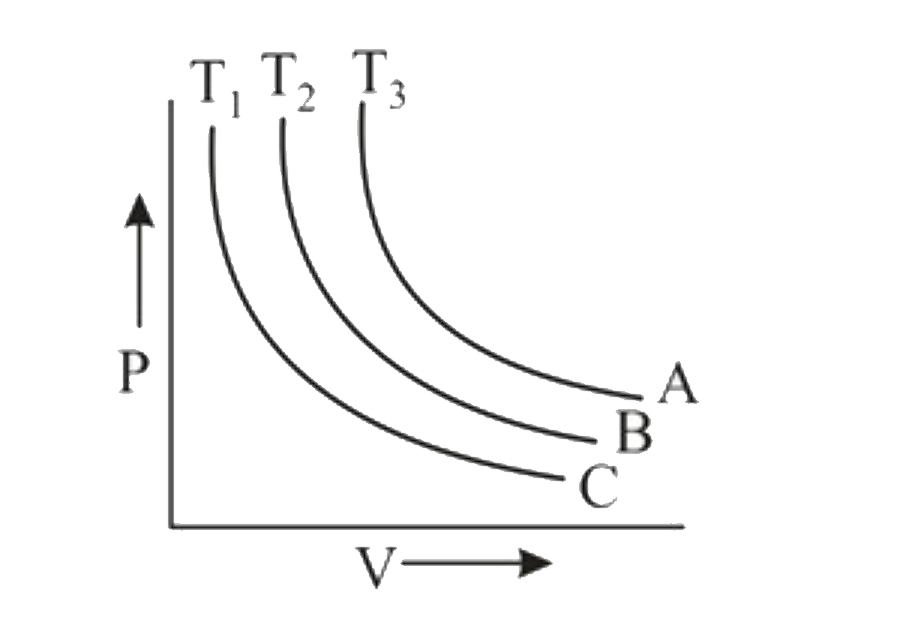
The correct order of the temperature will be
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View Solutionv1andv2 are the velocities of sound at the same temperature in two monoatomic gases of densities ρ1andρ2 respectively. If ρ1ρ2=14 then the ratio of velocities v1andv2 is
View SolutionThe velocities of sound at same temperature in two monoatomic gases densities ρ1 and ρ2 are v1 and v2 repectively , if ρ1ρ2=4, then the value of v1v2 will be
View SolutionIn the following P-V diagram two adiabatics cut two isothermals at temperature T1andT2 (fig). The value of VaVd will be
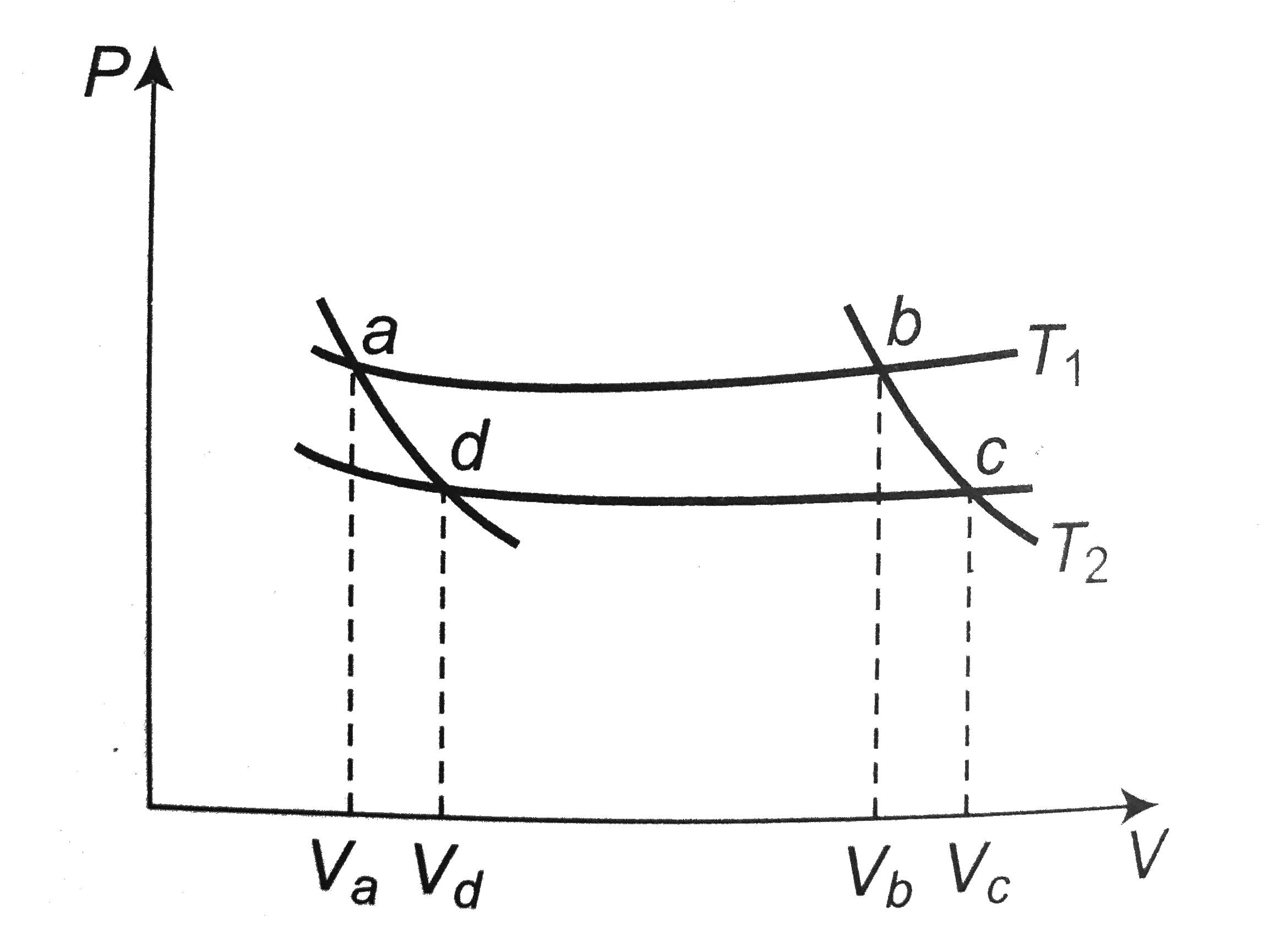
View Solution