Two bodies of masses (m1) and (m2) are droppded from heithts h1 and h2, respectively. They reach the ground after time t1 and t2 and strike the ground with v1 and v2, respectively Choose the correct relations from the following.
t1t2=√h1h2
t1t2=√h2h1
v1v2=√h1h2
v1v2=h2h1
The correct Answer is:A, C
To solve the problem, we will analyze the motion of the two bodies dropped from heights h1 and h2. We will use the equations of motion under uniform acceleration due to gravity.
1. Identify the Initial Conditions:
- Both bodies are dropped from rest, so their initial velocities u1 and u2 are 0.
- The acceleration g is constant for both bodies.
2. Use the Equation of Motion for Height:
- The equation of motion for an object in free fall is given by:
h=ut+12gt2
- For the first body:
h1=0⋅t1+12gt21⇒h1=12gt21
- For the second body:
h2=0⋅t2+12gt22⇒h2=12gt22
3. Establish the Ratio of Heights:
- Taking the ratio of h1 and h2:
h1h2=12gt2112gt22=t21t22
- This implies:
t1t2=√h1h2
4. Use the Equation of Motion for Velocity:
- The final velocity of an object in free fall is given by:
v=u+gt
- For the first body:
v1=0+gt1⇒v1=gt1
- For the second body:
v2=0+gt2⇒v2=gt2
5. Establish the Ratio of Velocities:
- Taking the ratio of v1 and v2:
v1v2=gt1gt2=t1t2
- This implies:
v1v2=√h1h2
6. Conclusion:
- From the above calculations, we have established the following relationships:
- h1h2=(t1t2)2
- v1v2=√h1h2
- Therefore, the correct options are:
- Option 1: h1h2=(t1t2)2
- Option 3: v1v2=√h1h2
- Both bodies are dropped from rest, so their initial velocities u1 and u2 are 0.
- The acceleration g is constant for both bodies.
- The equation of motion for an object in free fall is given by:
h=ut+12gt2
- For the first body:
h1=0⋅t1+12gt21⇒h1=12gt21
- For the second body:
h2=0⋅t2+12gt22⇒h2=12gt22
- Taking the ratio of h1 and h2:
h1h2=12gt2112gt22=t21t22
- This implies:
t1t2=√h1h2
- The final velocity of an object in free fall is given by:
v=u+gt
- For the first body:
v1=0+gt1⇒v1=gt1
- For the second body:
v2=0+gt2⇒v2=gt2
- Taking the ratio of v1 and v2:
v1v2=gt1gt2=t1t2
- This implies:
v1v2=√h1h2
- From the above calculations, we have established the following relationships:
- h1h2=(t1t2)2
- v1v2=√h1h2
- Therefore, the correct options are:
- Option 1: h1h2=(t1t2)2
- Option 3: v1v2=√h1h2
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Assertion-reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Linked Comprehension
30 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Two bodies of masses m1andm2 fall from heights h1andh2 respectively. The ratio of their velocities when the hit the ground is
View SolutionThe area of hole (1) is A1 and of hole (2) is A2. The velocity of efflux and range of liquid is v1,v2andx1,x2 for holes (1) and (2) respectively. The time taken by liquid, jet to reach the ground from holes (1) and (2) are t1andt2 respectively. Cross section of tank is very very large compared to size of holes.
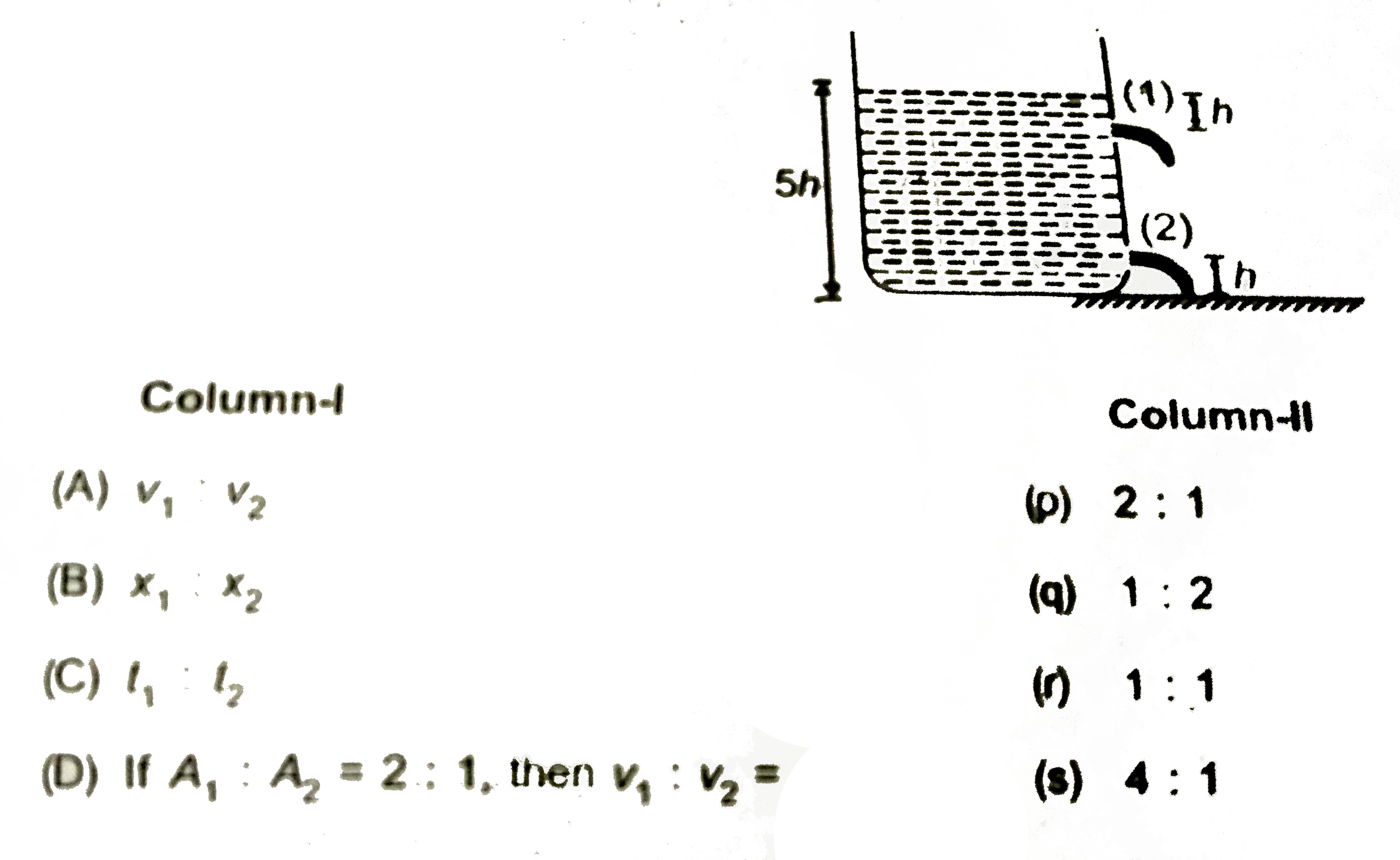
Column-IColumn-II(A)v1:v2(p)2:1(B)x1:x2(q)1:2(C)t1:t2(r)1:1(D)ifA1:A2=2:1,thenv1:v2=(s)4:1
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionTwo bodies of masses m1 and m2 are acted upon by a constant force F for a time t . They start from rest and acquire kinetic energies K1 and K2 respectively. Then K1K2 is :
View SolutionTwo satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionIn the figure shown , the tension is strings are T1 and T2 for figure (1) and (2) respectively and acceleration of mass m are a1 and a2 for figure (1) and (2) respectively.Select the correct option
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View Solution
