For an ideal gas, the graph representing the variation of the speed of sound (v) in a gas, with the r.m.s. speed (vrms) of its gas molecules with be


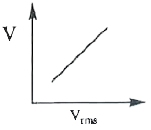
The correct Answer is:C
To solve the problem of how the speed of sound (v) in an ideal gas varies with the root mean square speed (v_rms) of its gas molecules, we can follow these steps:
Step 1: Understand the formulas
The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where:
- R is the universal gas constant,
- T is the absolute temperature in Kelvin,
- M is the molar mass of the gas.
The speed of sound (v_s) in an ideal gas is given by:
vs=√γRTM
where:
- γ is the adiabatic index (ratio of specific heats, Cp/Cv).
Step 2: Relate the two speeds
To find the relationship between vrms and vs, we can divide the two equations:
vrmsvs=√3RTM√γRTM
In this expression, R, T, and M will cancel out:
vrmsvs=√3γ
Step 3: Express vrms in terms of vs
From the above relationship, we can express vrms in terms of vs:
vrms=vs⋅√3γ
This shows that vrms is directly proportional to vs.
Step 4: Graphical representation
Since vrms is proportional to vs, we can represent this relationship graphically. If we let vrms be on the x-axis and vs be on the y-axis, the equation can be rearranged to:
vs=1√3γvrms
This is a linear equation of the form y=mx, where m is a constant. Therefore, the graph will be a straight line passing through the origin.
Conclusion
The graph representing the variation of the speed of sound (v) in a gas with the root mean square speed (v_rms) of its gas molecules will be a straight line.
The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where:
- R is the universal gas constant,
- T is the absolute temperature in Kelvin,
- M is the molar mass of the gas.
vs=√γRTM
where:
- γ is the adiabatic index (ratio of specific heats, Cp/Cv).
To find the relationship between vrms and vs, we can divide the two equations:
vrmsvs=√3RTM√γRTM
In this expression, R, T, and M will cancel out:
vrmsvs=√3γ
From the above relationship, we can express vrms in terms of vs:
vrms=vs⋅√3γ
This shows that vrms is directly proportional to vs.
Since vrms is proportional to vs, we can represent this relationship graphically. If we let vrms be on the x-axis and vs be on the y-axis, the equation can be rearranged to:
vs=1√3γvrms
This is a linear equation of the form y=mx, where m is a constant. Therefore, the graph will be a straight line passing through the origin.
The graph representing the variation of the speed of sound (v) in a gas with the root mean square speed (v_rms) of its gas molecules will be a straight line.
Topper's Solved these Questions
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Pipes)
Explore 13 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Beats : )
Explore 20 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Strings (Speed of a travelling wave:))
Explore 23 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:PROBLEMS (LEVEL - II)
Explore 33 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -III (POLARISITION)
Explore 10 Videos
Similar Questions
Knowledge Check
A student plotted the following four graphs representing the variation of velocity of sound in a gas with the pressure P. Whic one is correct?
A B
B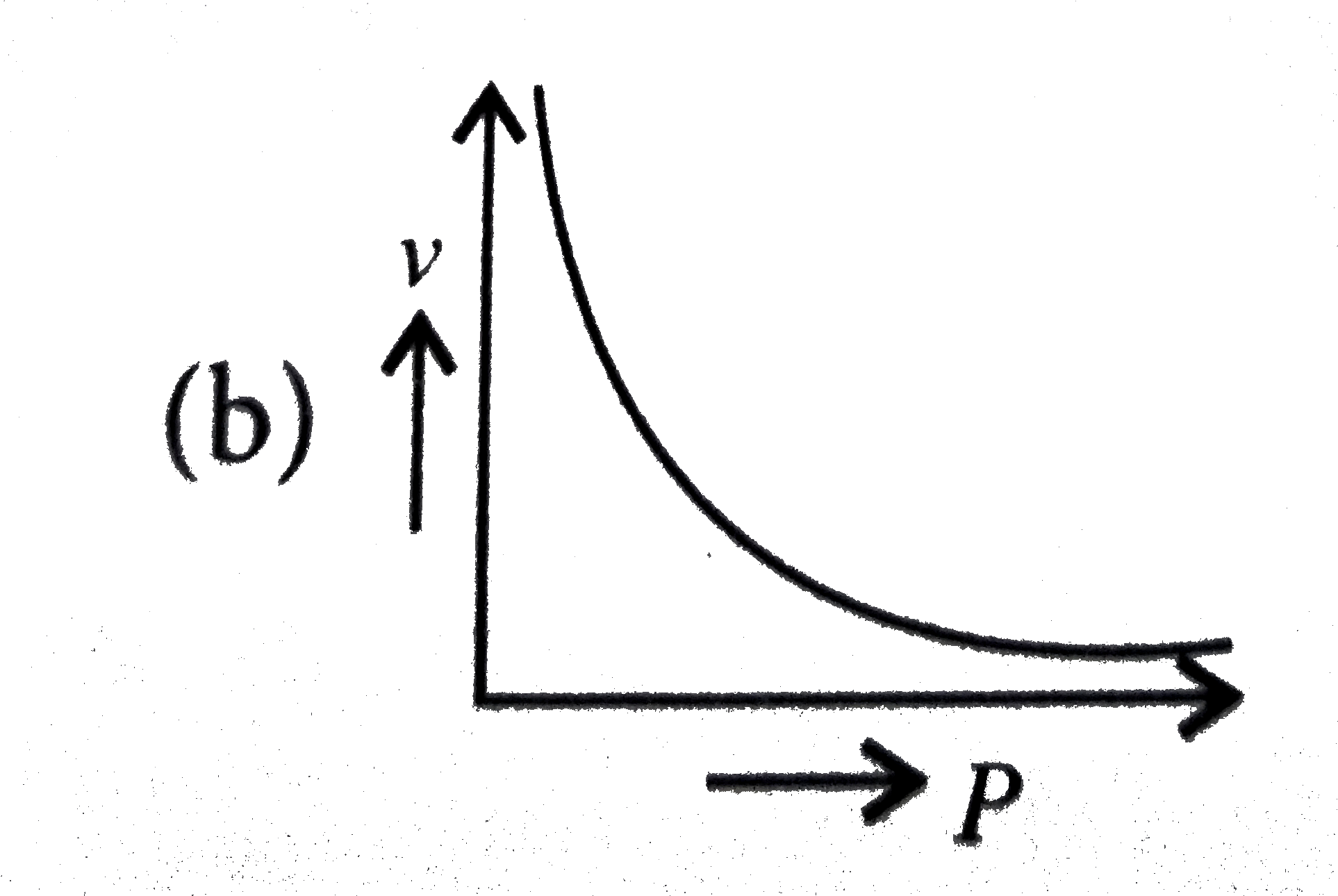 C
C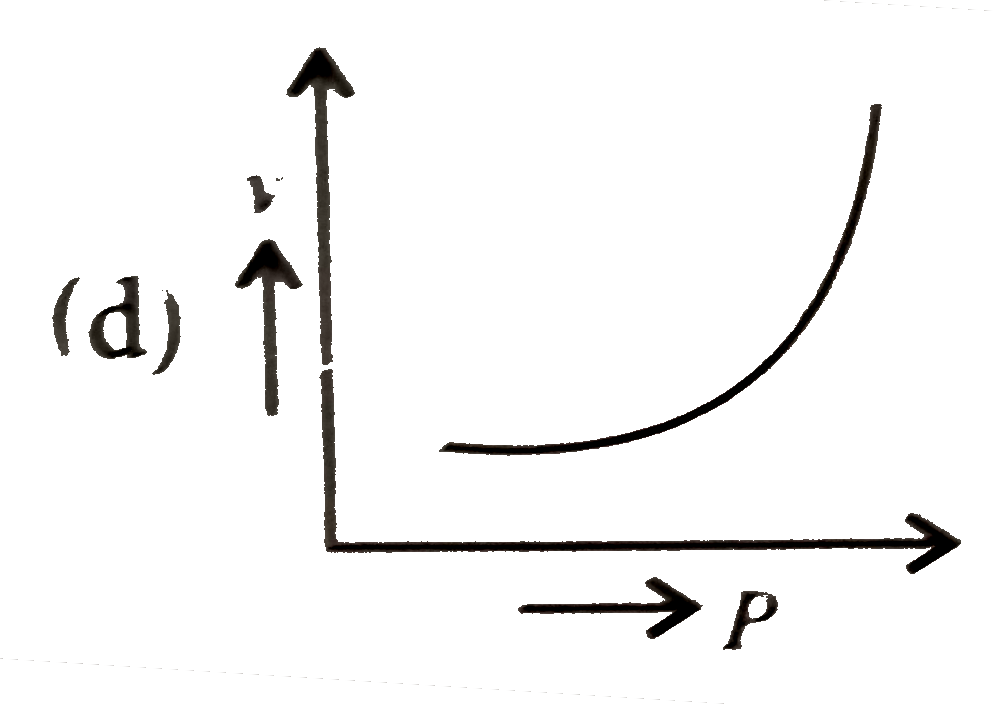 D
D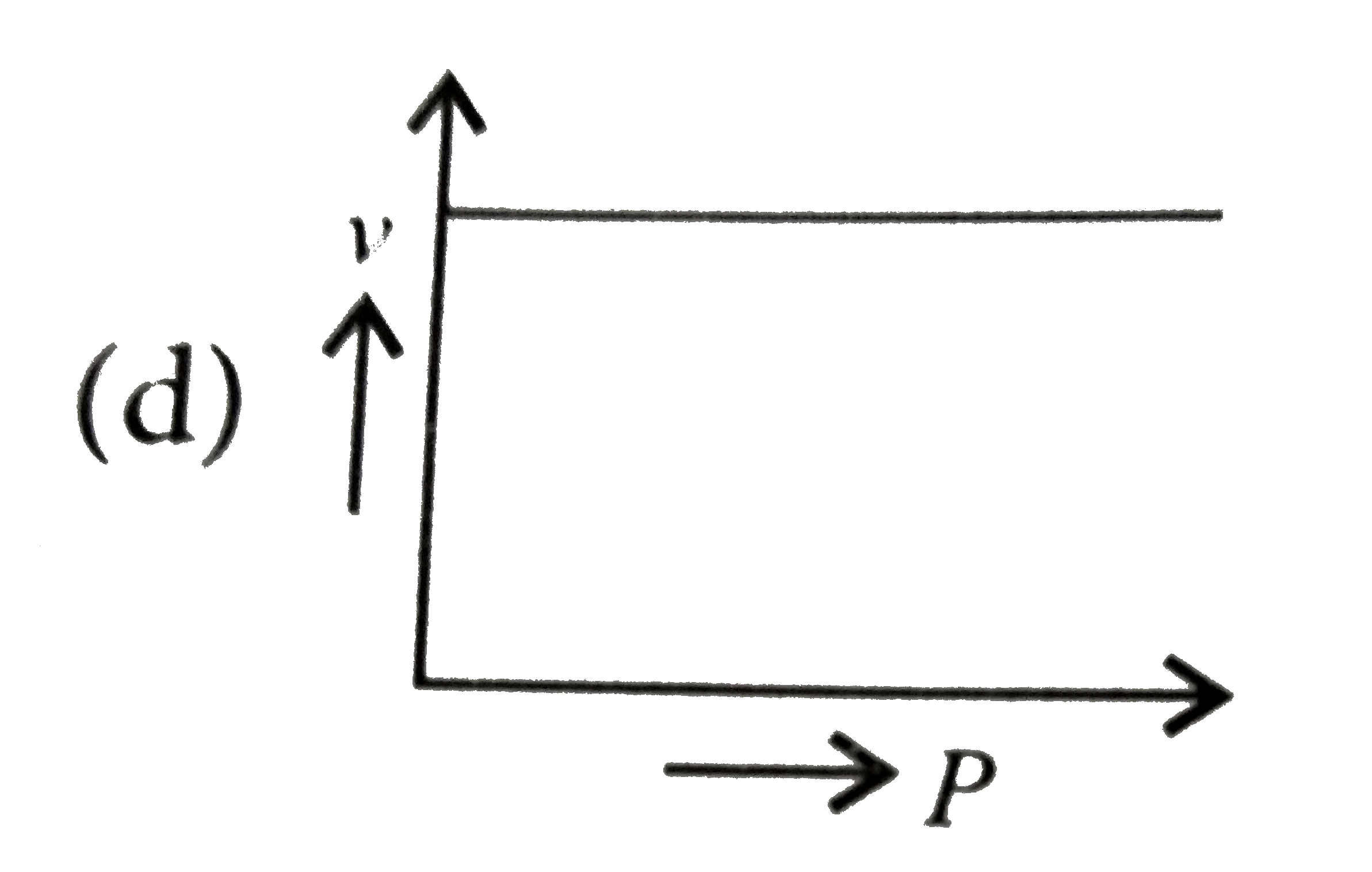
If vrms is the rms speed of molecules in a gas and v is the speed of sound waves in the gas, then the ratio vrmsv is
A√3γB√γ3C√3γD√3γ
Define average speed and r.m.s. speed of a gas molecule.
View SolutionFind the rms speed of oxygen molecules in a gas at 300K.
View SolutionThe ratio of the speed of sound in nitrogen gas to that in helium gas, at 300K is
View SolutionThe ratio of the speed of sound in nitrogen gas to that in helium gas, at 300K is
View SolutionThe r.m.s speed of the molecules of an ideal gas Is V0 If pressure of the gas is halved but temperature is kept constant then r.m.s. speed of the gas molecule will be
View SolutionSpeed of sound in a gas at constant temperature depends on
View Solution