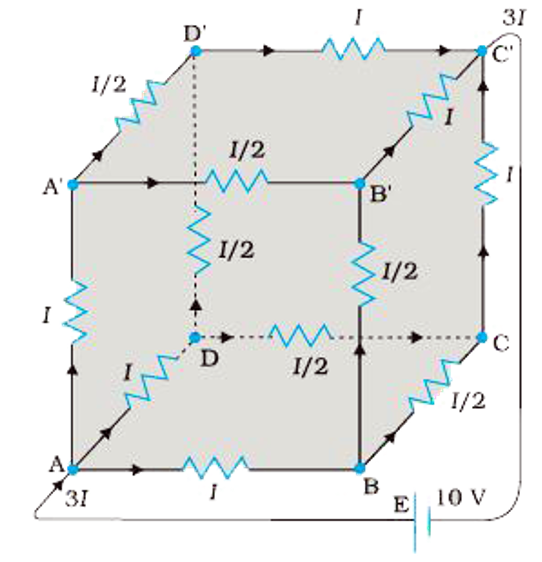
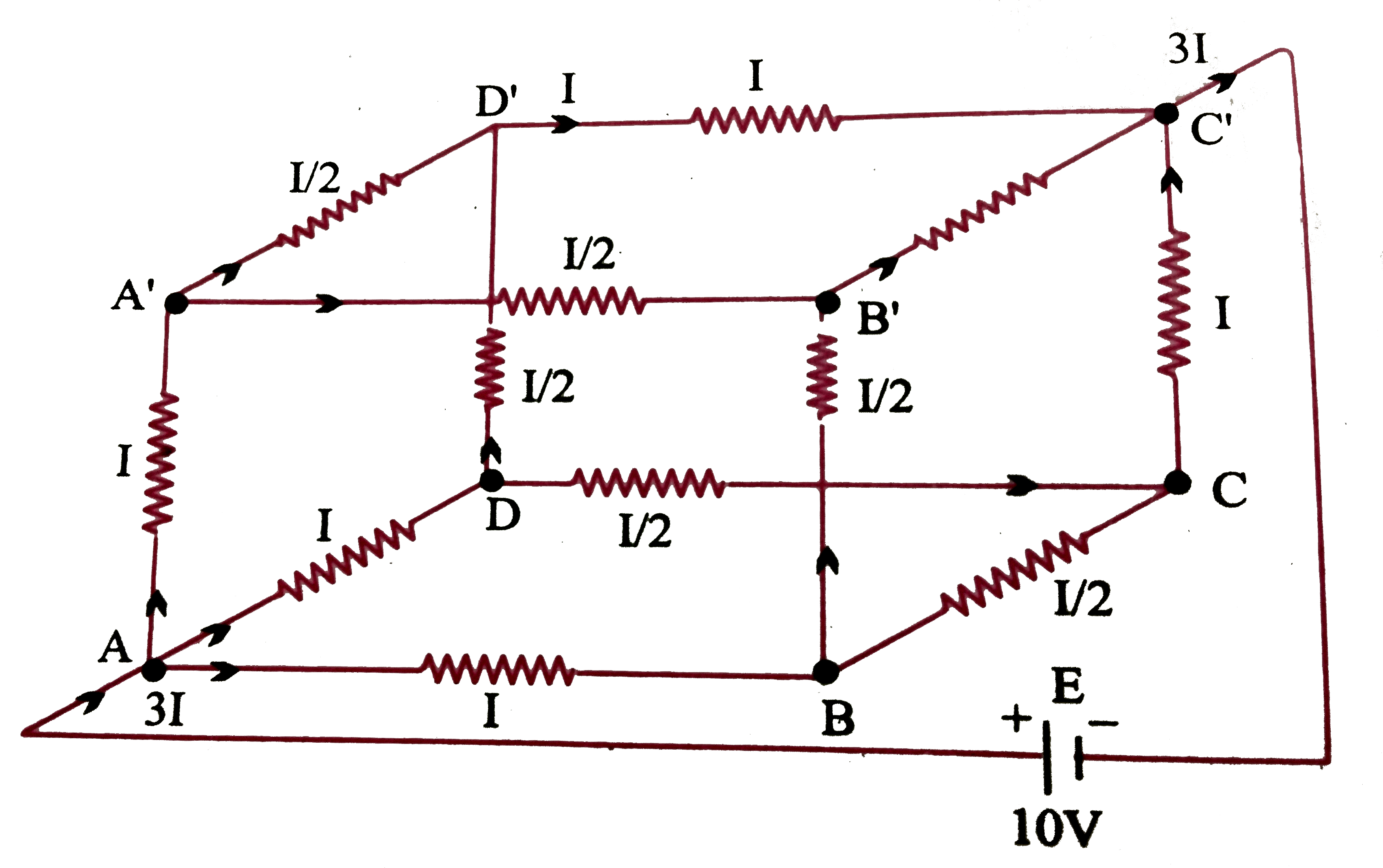
A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
 Solution in Tamil
Solution in Tamil
The network is not reducible to a simpleseries and parallel combinations of resistors.There is, however, a clear symmetry in the problem which we can exploit to obtain theequivalent resistance of the network.
The paths AA., AD and AB are obviously symmetrically placed in the network. Thus, the current in each must be the same, say, I. Further, at the corners A., B and D, the incoming current I must split equally into the two outgoing branches. In this manner, the current in all the 12 edges of the cube are easily written down in terms of I, using Kirchhoff.s first rule and the symmetry in the problem.
Next take a closed loop, say, ABCC.EA, and
apply Kirchhoff.s second rule:−IR−(12)IR−IR+ε=0
where R is the resistance of each edge and εthe emf of battery. Thus, ε=52IR
The equivalent resistance Req of the network is Req=ε31=56R
ForR=1Ω,Req=(56)Ωand forεon=10V, the total current (=31) in the network is 31=10V(56)Ω=12A,i.e.,=4
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NEW JOYTHI PUBLICATIONChapter:CURRENT ELECTRICITYExercise:SOLUTION TO EXERCISES FROM NCERT TEXT
Explore 24 Videos
- CURRENT ELECTRICITYBook:NEW JOYTHI PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS FOR SELF ASSESSMENT
Explore 25 Videos
- ATOMSBook:NEW JOYTHI PUBLICATIONChapter:ATOMSExercise:COMPETITIVE EXAM CORNER
Explore 5 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NEW JOYTHI PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:COMPETITIVE EXAM CORNER
Explore 15 Videos
Similar Questions
The storage battery of a car has an emf of 12 V.if the internal resistance of the battery is 0.4Ω,what is the maximum current that can be drawn from the battery>
View SolutionThe density of electrons in copper is 8.4×1022percm3? Calculate the drift velocity of electrons in a copper wire of 2mm2- area of cross section and carries a current of 0.15 A.
View SolutionThe set which represents the isotope , isobar, isotone respectively is
View SolutionIf 'm' is the mass of an electron and 'c' is the speed of light, the ratio of the wavelength of a photon of energy E to that of the electron of the same energy is
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
View Solution10 V तथा नगण्य आंतरिक प्रतिरोध की बैटरी एक घनीय परिपथ जाल ( नेटवर्क ) के "विकदत" सम्मुख कोनो से जुडी है परिपथ जाल में 1PΩ प्रतिरोध के 12 प्रतिरोधक है ( चित्र 3 .23 ) l परिपथ जाल का समतुल्य प्रतिरोध तथा धन के प्रत्येक के अनुदिश विधुत धारा ज्ञात कीजिए l
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1 Omega , a shown in fig. (a) complete the equivalent resistance of the network.
View Solution10 V तथा नगण्य आंतरिक प्रतिरोध कि बैटरी एक घनीय परिपथ जाल ( नेटवर्क ) के विकर्णताः सम्मुख कोनो से जुडी है । निम्न परिपथ जाल में 1Ω प्रतिरोध के 12 प्रतिरोधक है । परिपथ जाल का समतुल्य प्रतिरोध तथा घन के प्रत्येक किनारे के अनुदिश विद्युत धारा ज्ञात कीजिए ।
View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Omega as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops V_(BC) and V_(CD)
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Omega 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
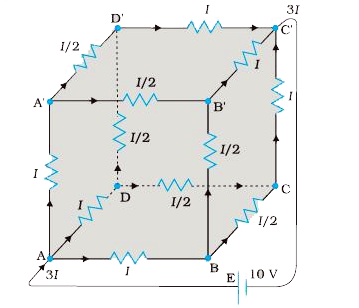
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.

View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
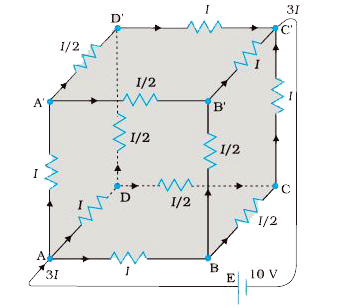
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
View Solution