Twelve wires, each of resistance are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
and 12A
and 12 A
4A
and 4A
The correct Answer is:A
Let R' be the resistance between point A and H.
...(i)
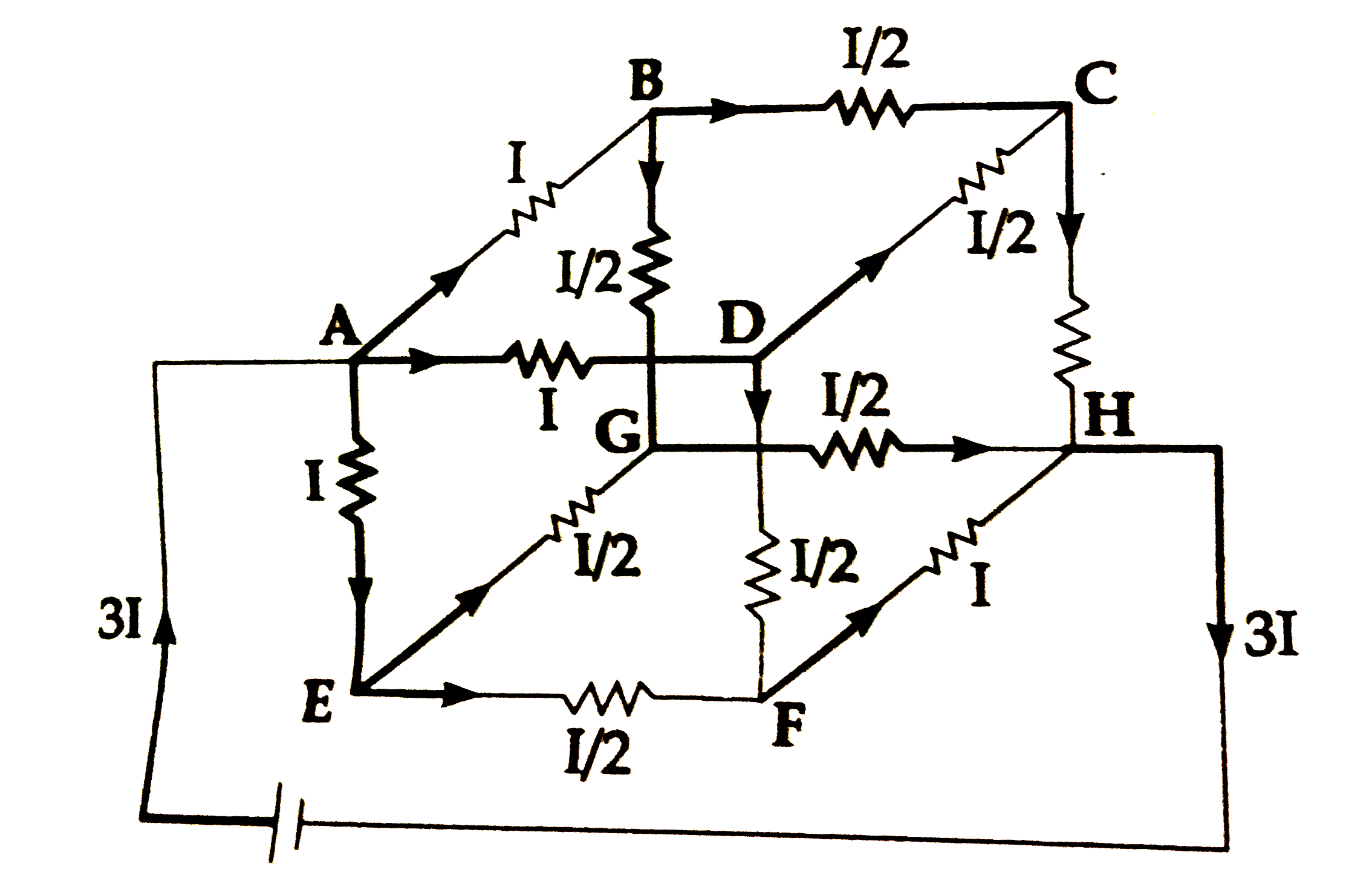
From figure,
... (ii)
From equation (i) and (ii) we have,
.
From figure,
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NIKITA PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Multiple Choice Questions
Explore 314 Videos
- COMMUNICATION SYSTEMSBook:NIKITA PUBLICATIONChapter:COMMUNICATION SYSTEMSExercise:Multiple Choice Questions (Examples for Practice)
Explore 8 Videos
- ELASTICITYBook:NIKITA PUBLICATIONChapter:ELASTICITYExercise:MCQ
Explore 314 Videos
Similar Questions
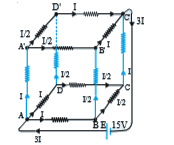
A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
Knowledge Check
Twelve wires each of resistance 6Ω are connected to from a cube as shown in the adjoining figure. The current enters at a cornet A and leaves at erhe diagonally opposite corner G. The equivalent resistance across the corners A and G is
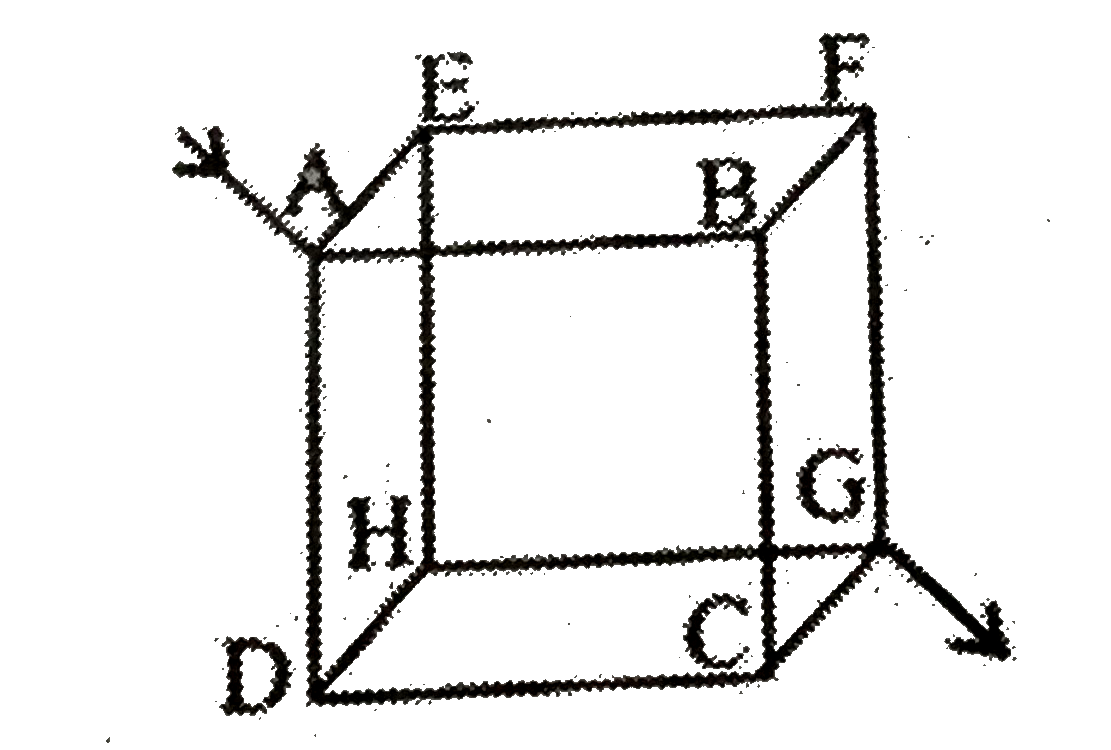 A12ΩB6ΩC3ΩD5Ω
A12ΩB6ΩC3ΩD5ΩTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
A5 ohmB10 ohmC20 ohmD5/4 ohm
A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.

View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
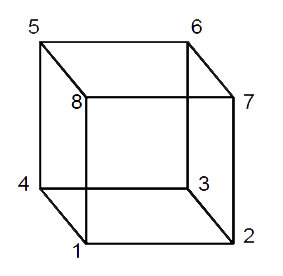
When current enters at 1 and leaves at 2
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
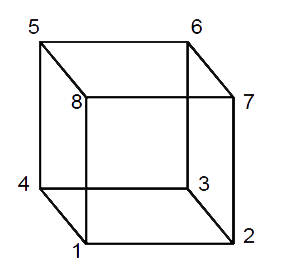
When current enters at 1 and leaves at 3
View SolutionTwelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View Solution