A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
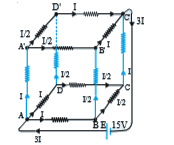
Let ABCDKLMN be the skeleton cube formed by joining twelve equal wires each of resistance r. Let the current enter the cube at corner A and after passing through all twelve wires, let the current leave at N, a corner diagonally oppsoite to corner A.
For the sake of convenience, let us suppose that the total current is 6I. At A, this current is divided into three equal parts each (2I) along AB,AD and AL as the resistance along these paths are equal. At into two equal parts each equal to i because resistance along the two paths are eaual. Thus, the distribution of current in the various arms of skelton cube is shown according to Kirchhoff's First rule. The current leaving the cube at N is again 6I. If ε is the emf of the battery used, then applying Kirchhoff's Second rule to the closed circuit ALKN ε A, we get
2Ir+Ir+2Ir=εor5Ir=ε
Where ε is the e.m.f. of the cell of negligible internal resistance.
If R is the resistance of the cube between the diagonally opposite corners A and N, then according to Ohm's Law, we have
6I×R=ε
From (i) and (ii), 6IR=5IrorR=56r
Here, r=1Ω, so R=56×1=56Ω
Current through battery =voltage of batterytotal resistance
=105/6=12A

Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
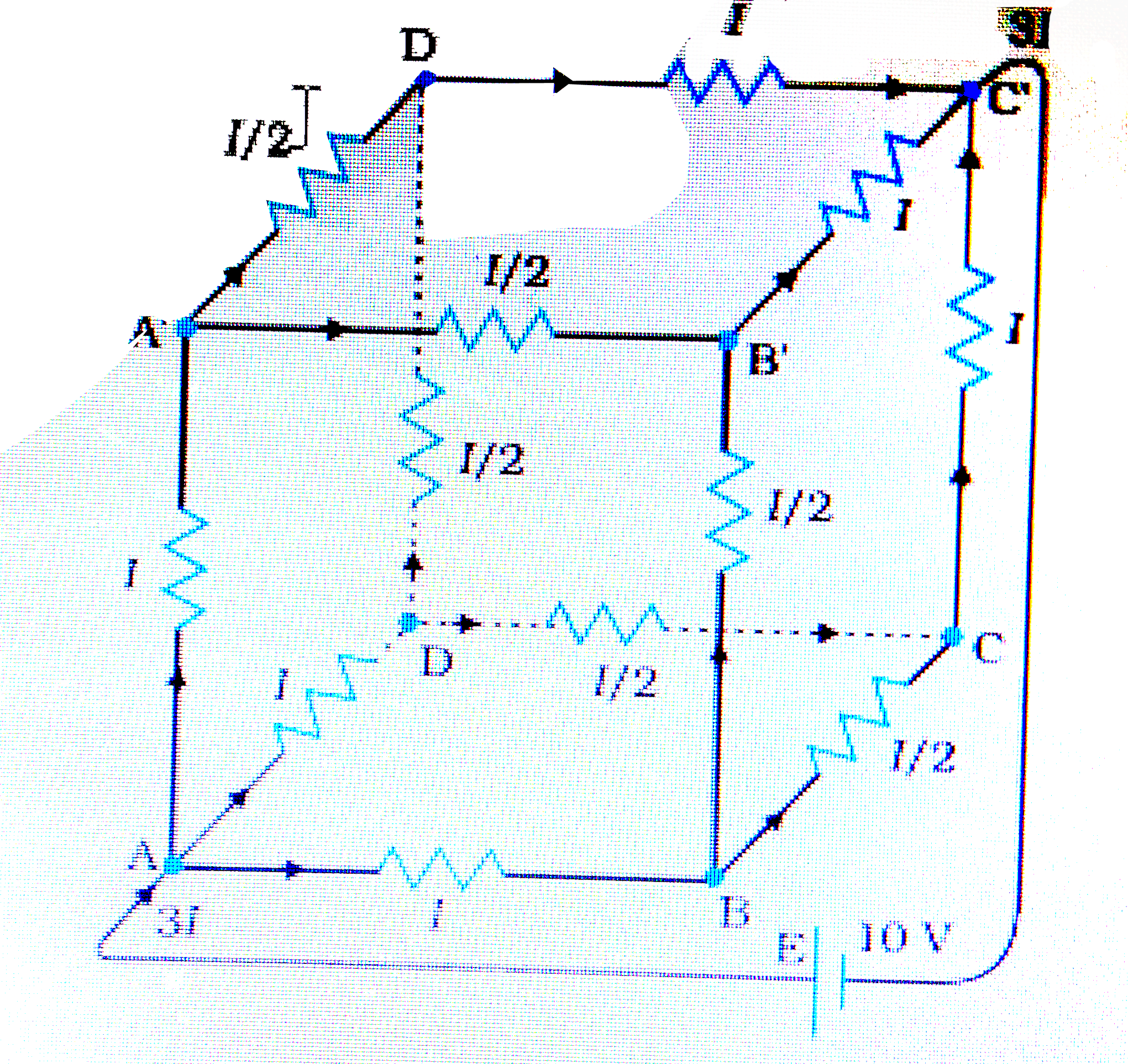
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.

View Solution
Knowledge Check
Twelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4AThree resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
A1.33ΩB3.0ΩC6.0ΩD12.0ΩThe figure shows a network of resistor each having value 12Ω. Find the equivalent resistance between points A and B.
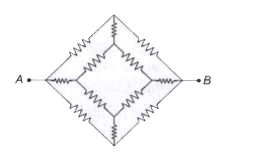 A9ΩB125ΩC8ΩD113Ω
A9ΩB125ΩC8ΩD113Ω
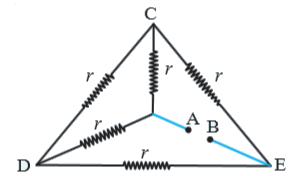
In the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionThe terminals of a battery of emf 3 V and internal resistance 2.5Ω are joined to the diagonally opposite corners of a cubical skeleton frame of 12 wires, each of resistance 3Ω. Find the current in the battery.
View SolutionIn the given network of resistors, each of resistance R, calculate the equivalent resistance between the junctions A and E

View SolutionIn the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–

View Solution

