Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
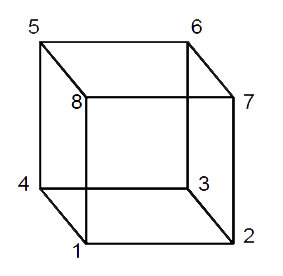
When current enters at 1 and leaves at 2
Here 3,7 are equipotential surface (if we move from 1→3,7 we have along face and 2,→3,7 we move along edge) similarly 4,8 are equipotential surface.
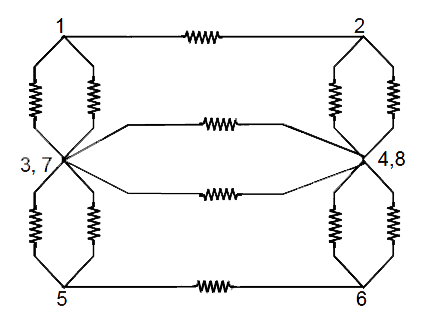
Req=7R12
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -1 (SECTION -A Definition of Current , Current Density , Drift Velocity )
Explore 8 Videos
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -1(SECTION B- Resistance & resistivity , Ohms law +VI (Volt - curr.) Characteristics + Colour Code + Temp . Dependence
Explore 8 Videos
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -3 SECTION -B (PREVIOUS YEAR PROBLEMS JEE MAIN)
Explore 42 Videos
- CONSTRAINED MOTION Book:MOTIONChapter:CONSTRAINED MOTION Exercise:EXAMPLES
Explore 12 Videos
- ELASTICITYBook:MOTIONChapter:ELASTICITYExercise:EXERCISE -3
Explore 60 Videos
Similar Questions
Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
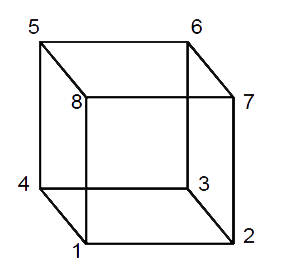
When current enters at 1 and leaves at 3
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
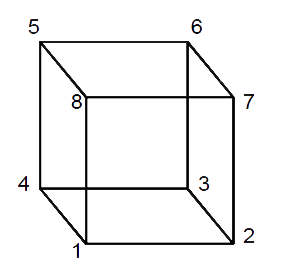
When current enters at 1 & leaves at 6 (body diagonal)
View Solution
Knowledge Check
Three resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
A1.33ΩB3.0ΩC6.0ΩD12.0ΩFive equal resistances each of value R are connected in a form shown in the following figure. The equivalent resistance of the network
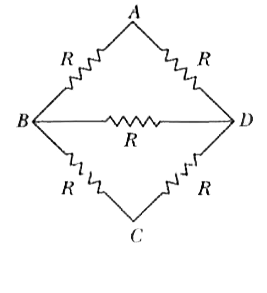 ABetween points B and D is R/2BBetween points A and C is RCBetween points B and D is RDBetween points A and C is R/2
ABetween points B and D is R/2BBetween points A and C is RCBetween points B and D is RDBetween points A and C is R/2Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
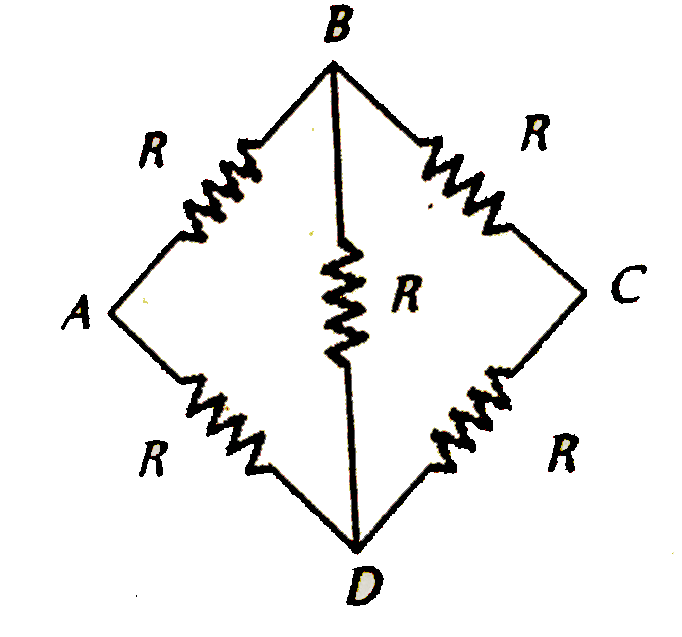 ABetween the points B and D is RBBetween the points B and D is R2CBetween the points A and C is RDBetween the points A and C is R2
ABetween the points B and D is RBBetween the points B and D is R2CBetween the points A and C is RDBetween the points A and C is R2
Five equal resistors each of RΩ are connected in a network. Calculate the equivalent resistance between the points A and B.

View SolutionThree resistors, each of resistance 12Ω, are connected in parallel. What is the equivalent resistance ?
View SolutionThese resistors of 10Ω,15Ωand5Ω are connected in parallel. Find their equivalent resistance.
View SolutionThe equivalent resistance of network of three 2Ω resistors can not be
View SolutionThree equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
View Solution