Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
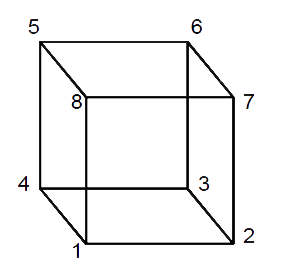
When current enters at 1 & leaves at 6 (body diagonal)
Here 2,4,8 are equipotential points (if we move from 1→2,4,8 it comes along the edge & 6→2,4,8 it comes along face diagonal). Similarly 3,5,7 are equipotential points.
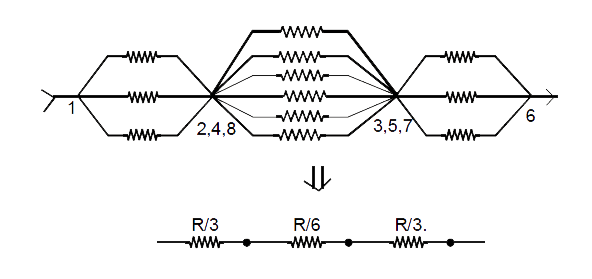
Req=5R6
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -1 (SECTION -A Definition of Current , Current Density , Drift Velocity )
8 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -1(SECTION B- Resistance & resistivity , Ohms law +VI (Volt - curr.) Characteristics + Colour Code + Temp . Dependence
8 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 SECTION -B (PREVIOUS YEAR PROBLEMS JEE MAIN)
42 Videos
- CONSTRAINED MOTION BOOK - MOTIONCHAPTER - CONSTRAINED MOTION EXERCISE - EXAMPLES
12 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
Similar Questions
Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
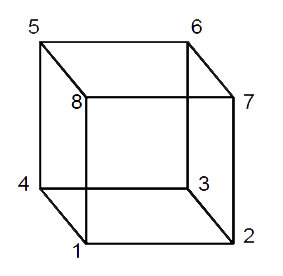
When current enters at 1 and leaves at 2
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
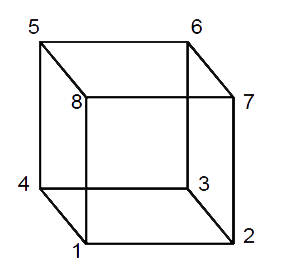
When current enters at 1 and leaves at 3
View Solution
Knowledge Check
Three resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
A1.33ΩB3.0ΩC6.0ΩD12.0ΩFive equal resistances each of value R are connected in a form shown in the following figure. The equivalent resistance of the network
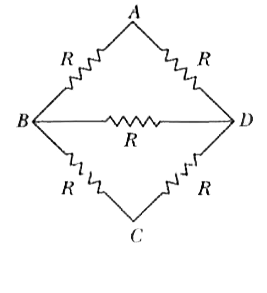 ABetween points B and D is R/2BBetween points A and C is RCBetween points B and D is RDBetween points A and C is R/2
ABetween points B and D is R/2BBetween points A and C is RCBetween points B and D is RDBetween points A and C is R/2Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
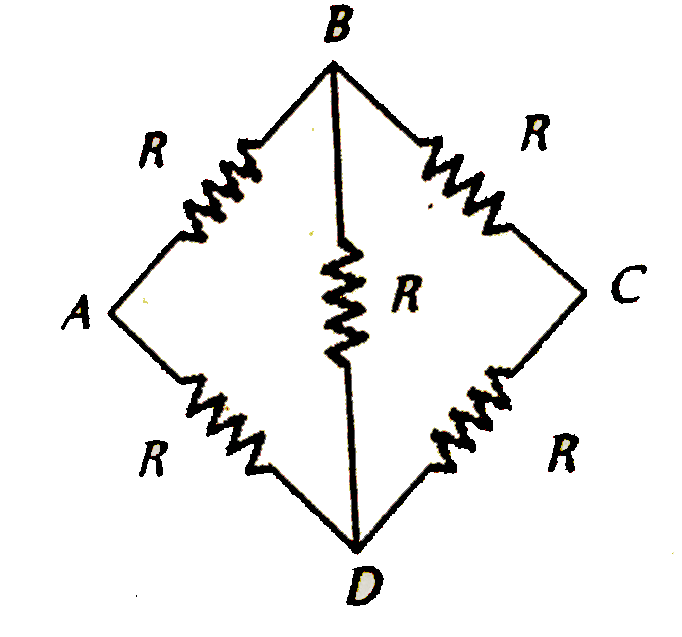 ABetween the points B and D is RBBetween the points B and D is R2CBetween the points A and C is RDBetween the points A and C is R2
ABetween the points B and D is RBBetween the points B and D is R2CBetween the points A and C is RDBetween the points A and C is R2
Five equal resistors each of RΩ are connected in a network. Calculate the equivalent resistance between the points A and B.

View SolutionThree resistors, each of resistance 12Ω, are connected in parallel. What is the equivalent resistance ?
View SolutionThese resistors of 10Ω,15Ωand5Ω are connected in parallel. Find their equivalent resistance.
View SolutionThree equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
View SolutionThree identical resistors, each of 6Ω are connected in parallel. The equivalent resistance of the combination will be ______.
View Solution
