A network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
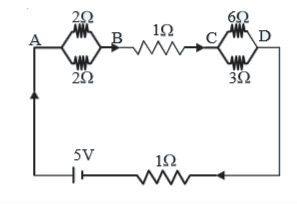
(a) The network is a simple series and parallel combination of resistors. First two 2Ω resistors in parallel are equivalent to a resistor =2x22+2=1Ω.
In the same way, the 3Ω and 6Ω resistors in parallel are equivalent to a resistor of ,
=6×36+3=2Omega<br>The≡a≤ntresistanceRofthe≠tworkisobta∈edbycomb∈∈gtheseresis→rs(2Omega and 4omega)with1Omega∈series,tˆis,<br>1+1+2+1=5Omega<br>(b)The→talcurrentI∈the∘uitis<br>I=(E)/(R)=(5)/(5)=1A<br>Consrtheresis→rsbetweenAandB.IfI_(1)isthecurrent∈o≠ofthe2Omegaresis→rsandI_(2)thecurrent∈theother,I_(1)xx 2=1_(2) xx2tˆis,I_(1)=I_(2)whichisotherwiseobviousomthesymmetryofthetwoarms.ButI_(1)+1_(2)=I=1A.Thus,1_(1)=I_(2)=(1)/(2)Atˆiscurrent∈each2Omegaresis→ris(1)/(2) A.Current∈1Omegaresis→rbetweenBandCwod––be1A.Now,consrtheresistancesbetweenCandD.IfI_(3)isthecurrent∈the6Omegaresis→r,andI_(4)∈the3Omegaresis→r,I_(3)xx6=I_(4)xx3i.e,I_(4)=2I_(3)<br>But,I_(3)+I_(4)=I=1A<br>Thus,I_(3)=((1)/(3))A,I_(4)=((2)/(3))A<br>(c)Thevo<a≥dropacrossABisV_(AB)=I_(1)xx2=(1)/(2)Axx2Omega=IV<br>Thevo<a≥dropacrossBCisV_(BC)=1Axx1Omega=1V <br>F∈ally,thevo<a≥acrossCDisV_(CD)=6OmegaxxI_(3)=6Omrgaxx((1)/(3))0A=2V
Similar Questions
A network of resistances is connected to a 16 V battery with internal resistance of 1Ω as shown in figure. (a) Compute the equivlaent resistance of the network. (b) Obtain the current in each resistor and (c ) obtain the voltage dropVAB,VBC and VCD.
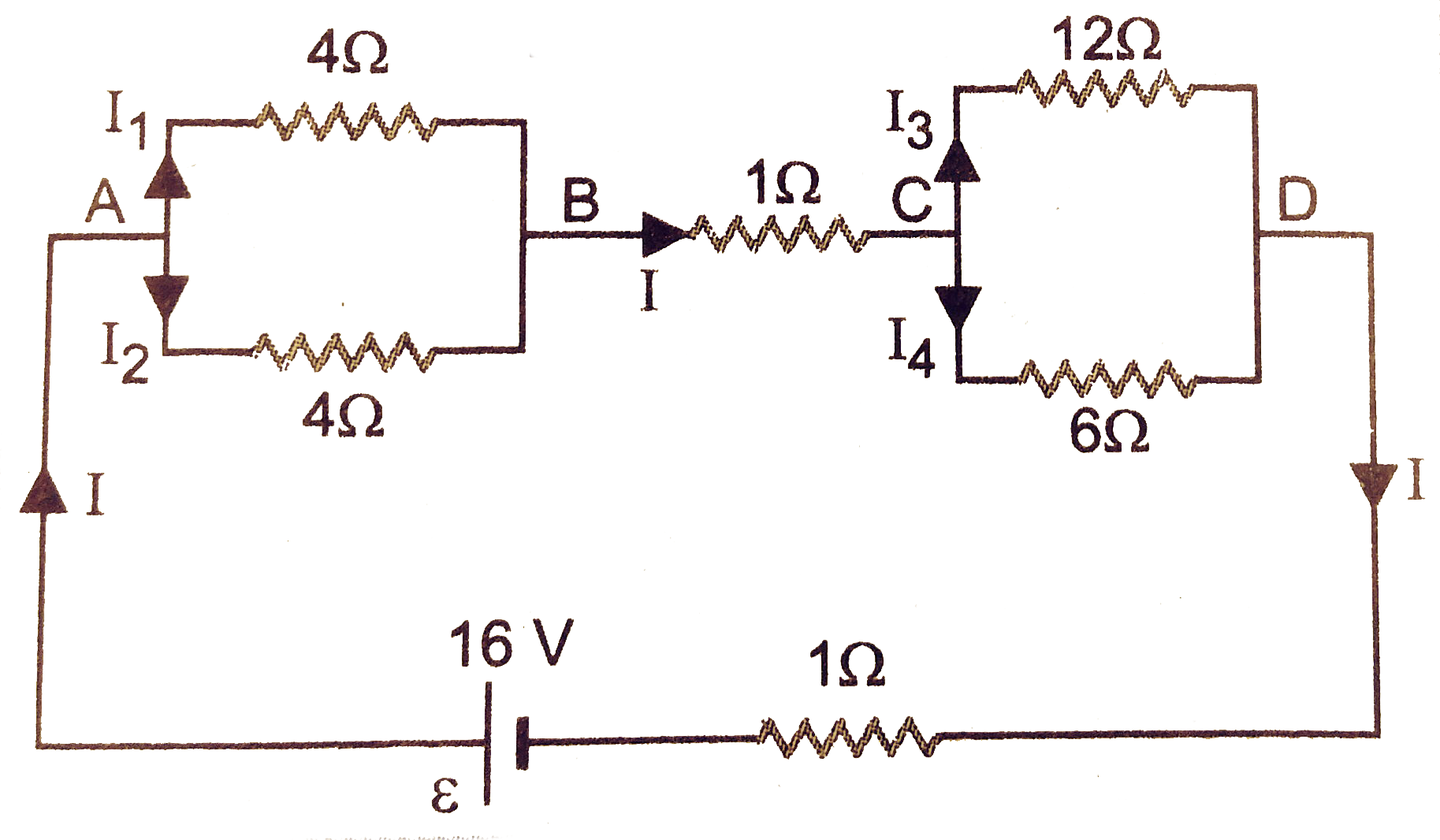
View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1Ω, as shown in Fig. 4.33.

(a) Compute epuivalent resistance of the network,
(b) obtain the current In in each resistor, and
(c ) obtain the voltage drops VAB,VBC and VCD.
View Solution
Knowledge Check
The equivalent resistance of network of three 4Ω resistors can not be
A12ΩB1.33ΩC6ΩD4ΩThe equivalent resistance of network of three 2Ω resistors can not be
A0.67B2ΩC3ΩD6ΩThe equivalent resistance of network of three 4Ω resistors can not be
A12ΩB1.33ΩC6ΩD4Ω

A network of resistors is connected to a battery of negligible internal resistance, as shown in figure. Calculate the equivalent resistance between the point A and D, and the value of the current I3.
View SolutionA resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
View SolutionThree resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
View Solution7 V battery with internal resistance 2Ωand3V battery with internal resistance 1Ω are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
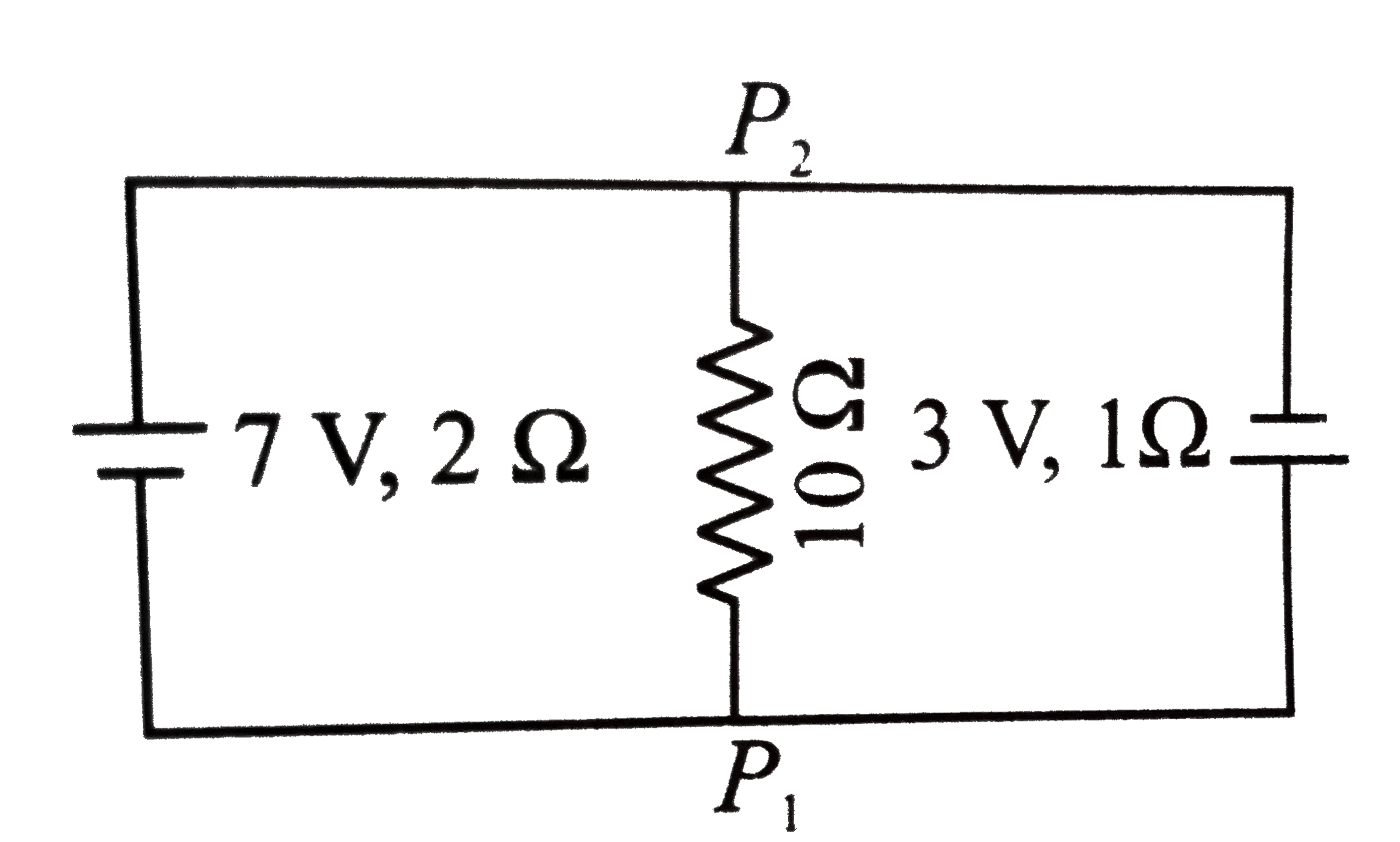
View Solution

