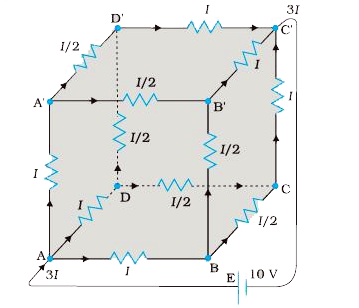
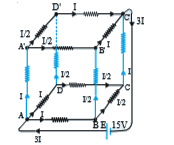
A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
 Solution in Telugu
Solution in Telugu
The network is not reducible to a simple series and parallel combinations of resistors. There is, however, a clear symmetry in the problem which we can exploit to obtain the equivalent resistance of the network.
The paths AA..AD and AB are obviously symmetrically placed in the network. Thus, the current in each must be the same, say, I. Further, at the corners A.,B and D, the incming current I must split equially into the two outgoing branches. In this manner, the current in all the 12 deges of the cube are esaily written down in terms of I, using kirchhoffs first rule and the symmetry in the problem.
Next take a closed loop, say. ABCCEA, and apply kirchhoffs second rule:
ε=52IR
The equivalent rsistance Req of the network is
Req=ε3I=56R
For R=1Ω,Req(5/6)Ωand for ∈=10V, the total current (=3I) in the network is
3I=10V(5/6)Ω=12A,i.e.,I=4A
The current following in each edge can now be read off from the
Similar Questions
A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
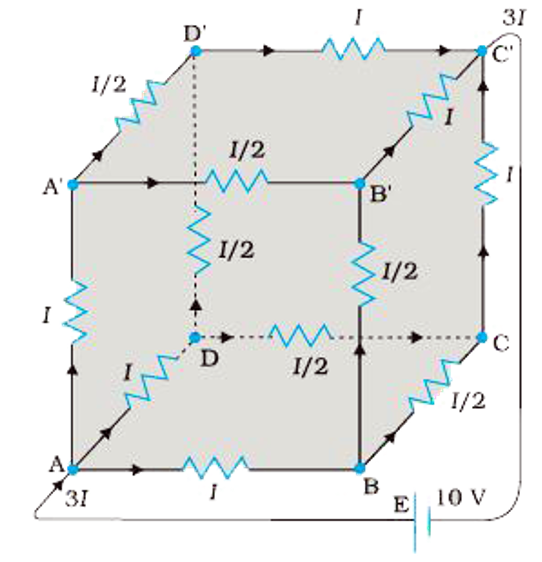
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
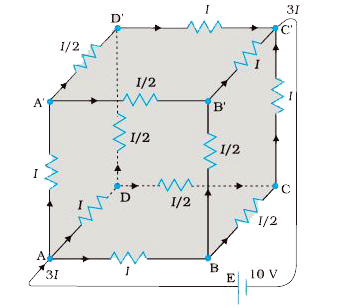
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.

View SolutionA network of Resistors is Connected to a 16V battery with internal resistance 1Omega as shown in Figure below. (a) Compute the equivalent resistance of the network (b) Calculate the total current in the circuit
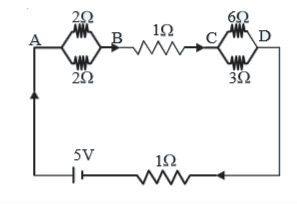
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω . Determine the equivalent resistance of the network and the current along each edge of the cube.
View Solution

