A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2 . The inner surface (a cylinder of length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2(θ1>θ2) .The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.Solution in Tamil
The correct Answer is:A, B, D
dQdt=Rate of flow heat
Lets us consider a strip at a distance r from the centre of thickness dr.
Qdt=K×2π×rd×dθdr
[dθ=tempareturedofferenceacrossthethick≠ssdr]
C=K×2π×rd×dθdr[c=θt]
c×drr=K2πddθ
Integrating
⇒C∫r2r1drr=K2πd∫θ1θ2dθ
⇒C[logr]r2r1=K2πd(θ1=θ2)
C(logr2−logr1)=K2πd(θ1=θ2)
⇒c=K2πd(θ1=θ2)log(r2/r1).

Topper's Solved these Questions
Similar Questions
A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registered at 140°F. What is the fall in temperature as registered by the centigrade thermometer ?
View SolutionThe steam point and the ice point of a mercury thermometer are marked as 80∘C and 20∘C. What will be the temperature in centigrade mercury scale when this thermometer reads 32∘C?
View SolutionFind the dimensions of
a. linear momentum
b. frequency and
c. pressure
View SolutionTwo thin metallic spherical shells of radii r1andr2(r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature θ1 .and the outer shell at temperature θ2(θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionA hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T_(2)gtT_(1)(b)the∈softhetubeisma∫a∈edattemperatureT_(1)andtheoutsisma∫a∈edatT_(2) .
View SolutionA stema pipe with a radius R1 is surrounded by an insulating jacket with an outer radius of R0 If the temperature of the inner (θ1) and outer (θ0) surface are fixed (θ1>θ0) find the heat flow through the jacket. (Apply the heat conduction euation to steady state radial heat flow corresponding to cylindrical symmetry) .
View SolutionCalculate thermal conductance for radial flow of an annular cylinder of length l and inner and outer radius r_(1) and r_(2) . Assume that thermal conductivity of the material is K
View SolutionCalculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r_(1) and r_(2) . Assume that thermal conductivity of the material is K
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are theta_(2) and theta_(1) respectively, (theta_(2) gt theta_(1)) The temperature at the interface is:
View Solutionदिखाए गए चित्रानुसार 3K तथा K उष्माचालकता गुणांक एवं क्रमशः d तथा 3d मोटाई वाले दो पदार्थो जो जोड़कर एक पट्टिका बनायी गयी है। उनके बाहरी सतहों के तापमान क्रमशः θ2 और θ1 है (θ2>θ1) अंतरपृष्ठ का तापमान है

View Solutionदिखाए गए चित्रानुसार 3K तथा K ऊष्माचालकता गुणांक एवं क्रमश: d तथा 3d मोटाई वाले दो पदार्थों को जोड़कर एक पट्टिका बनायी गयी है। उनके बाहरी सतहों के तापमान क्रमश: θ1 और θ2 हैं (θ2>θ1)। अंतरपृष्ठ का तापमान है
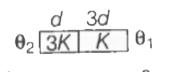
View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 .and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionA hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T2>T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2 .
View SolutionHeat flows radially outward through a spherical shell of outside radius R2 and inner radius R1. The temperature of inner surface of shell is θ1 and that of outer is θ2. At what radial distance from centre of shell the temperature is just half way between θ1 and θ2
View SolutionShow that are rate of flow of heat through a spherical shell , the inner and outer walls of which have radii r1 and r2 and are maintained at differnet unifrom temperature θ1 and θ2 respectievly , is given by H=4Kr1r2θ1−θ2r2−r1 where K is thermal conductivity of material of shell . He obtain the expression for temperature distributions.

View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View Solution
